Da REW Wiki.
Interpretare le risposte all’impulso, è una parte importante dell’analisi acustica. Una misurazione della risposta all'impulso ci può fornire una grande quantità di informazioni relative ad una stanza e in che modo il suono verrà riprodotto al suo interno. Può indicarci che tipi di trattamento potrebbero esserci di aiuto e se questi sono stati applicati correttamente per ottenere il migliore risultato. Questa pagina spiega le risposte all’impulso e le informazioni che da queste possono essere ricavate e in che modo REW può misurarle ed analizzarle.
Cos’è una risposta all’impulso?
Prima di poter andare molto lontano nell’interpretazione della risposta all’impulso, dobbiamo prima capire cos’è. La risposta all’impulso in sostanza è la registrazione del comportamento della stanza, in presenza di un suono estremamente breve, riprodotto ad un livello estremamente elevato – qualcosa tipo lo sparo di una pistola. La ragione per misurare la risposta all’impulso (con mezzi più adeguati rispetto allo sparo di una pistola), è che essa caratterizza completamente il sistema, costituito dagli altoparlanti e dalla stanza in cui questi si trovano, nel punto in cui il microfono di misura è stato collocato. Un’importante proprietà di un impulso, non intuitivamente ovvia, è che, potendolo scomporre in singole onde sinusoidali, vedremmo che contiene tutte le frequenze alla stessa ampiezza. Strano, ma vero. Questo significa che si può elaborare la risposta in frequenza di un sistema, determinando le componenti in frequenza che compongono la sua risposta all’impulso. REW fa questo con la Trasformata di Fourier della risposta all’impulso, che in sostanza consiste nella sua scomposizione nelle singole componenti in frequenza. Il grafico dell’ampiezza di ciascuna di esse, rappresenta la risposta in frequenza del sistema.
Quando una risposta all’impulso viene misurata utilizzando uno sweep logaritmico sinusoidale, la risposta lineare della stanza viene opportunamente separata dalla sua risposta non lineare. La porzione della risposta prima del picco all’istante=0, è in realtà dovuta alla distorsione del sistema. Guardando più attentamente da vicino, si possono vedere copie ridotte e compresse orizzontalmente della risposta principale all’impulso, ciascuna dovuta alla distorsione armonica. La prima relativa alla seconda armonica, poi la terza, la quarta, ecc. man mano che il tempo diventa più negativo. Il picco iniziale e il suo conseguente decadimento dopo l’istante = 0, rappresenta la risposta del sistema senza la distorsione.
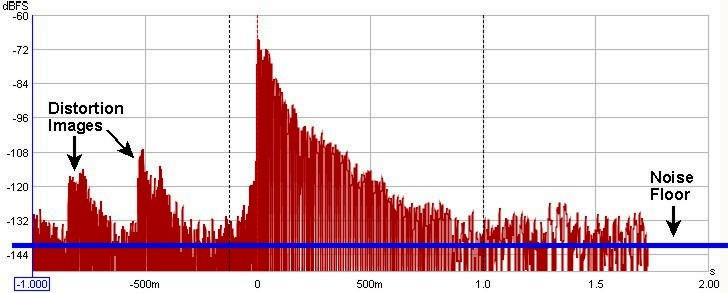
In un sistema perfetto con larghezza di banda infinita collocato in una stanza con il perimetro totalmente assorbente, la risposta all’impulso apparirebbe come un singolo picco all’istante = 0 e nient’altro. Per avvicinarci il più possibile, bisogna misurare la risposta di loopback della scheda audio. In un sistema reale, la limitata larghezza di banda crea fenomeni di distribuzione della risposta (in modo ancor più drammatico quando si effettuano misure su un subwoofer a causa della sua larghezza di banda molto limitata). Le riflessioni provenienti dalle pareti della stanza, si aggiungono alla risposta iniziale in tempi che corrispondono alla distanza che tali riflessioni hanno dovuto percorrere per raggiungere il microfono. Per esempio, nel caso di un microfono posto a 3 m. dagli altoparlanti, con una riflessione proveniente dal muro che deve percorrere circa 4,5 m., questa produrrebbe un picco (distribuito in funzione della natura della riflessione), 5ms più tardi dell’impulso iniziale, poichè il suono impiegherebbe tale intervallo di tempo per percorrere quella distanza aggiuntiva di circa 1,5 m.
Quando misuriamo le risposte a gamma intera di un sistema di altoparlanti (invece che di un subwoofer), le riflessioni sono più facili da individuare, grazie alla maggiore larghezza di banda del sistema e alla sua capacità di mantenere il picco dell’impulso (e le riflessioni), piuttosto stretto, ma sarà necessario aumentare l’asse temporale per poterle visualizzare. Per la loro individuazione, si consiglia di impostare l’asse Y in modo lineare (%FS anziché dBFS) e saranno più leggibili con ETC smoothing impostato a 0.
Finestre della Risposta all’Impulso
Dopo aver acquisito uno sweep, questo viene elaborato con la FFT per ricavare la risposta all’impulso del sistema e la corrispondente risposta in frequenza. I controlli utilizzati per regolare la posizione e la larghezza delle finestre di sinistra e di destra, usate per derivare la risposta in frequenza, sono accessibili premendo il pulsante "IR Windows", sulla barra degli strumenti.

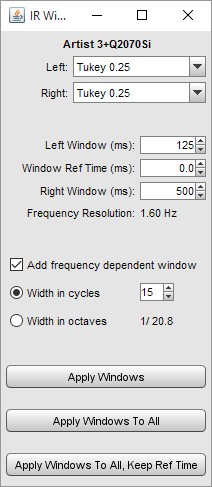
Le finestre e la regione della risposta all’impulso che esse coprono, possono essere visualizzate sul grafico dell’Impulso, selezionando "Window" e "Windowed", come mostrato nella figura qui sotto riportato. La posizione di riferimento per la finestra è generalmente il picco dell’impulso.
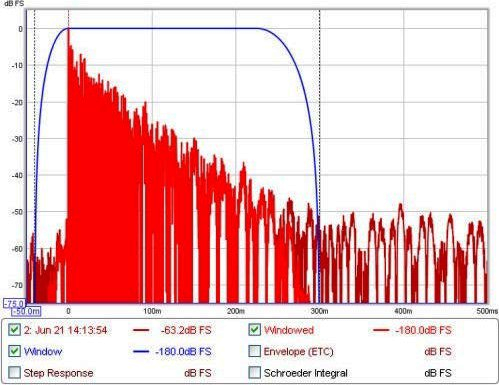
Solitamente, le impostazioni adatte per le finestre, sono quelle di default e non è necessario modificarle. In stanze di piccole dimensioni, potrebbe essere necessario diminuire la durata della finestra di destra, a circa 300-500ms. Se il grafico della risposta in frequenza appare rumoroso e frastagliato, provate a ridurre il periodo della finestra di destra e cliccate su "Apply Windows" per ricalcolare la risposta in frequenza. Nel caso di stanze molto grandi, la finestra può essere allargata per migliorare la risoluzione in frequenza.
La risoluzione della frequenza corrispondente alla durata totale della finestra corrente (destra e sinistra combinate), è mostrata sopra il pulsante Apply Windows: maggiore è la durata, maggiore è la risoluzione. Forme alternative possono essere selezionate per le finestre di sinistra e di destra, in modo indipendente.
Oltre alle finestre di sinistra e destra può essere applicata una finestra gaussiana dipendente dalla frequenza. Si tratta di una finestra la cui ampiezza varia inversamente alla frequenza, restringendosi progressivamente all'aumentare della stessa. La larghezza di tale finestra può essere specificata come numero di cicli o frazione di ottava. Se la larghezza è espressa in cicli, allora la larghezza (tra i punti di mezza ampiezza della finestra) a qualsiasi frequenza, sarà il numero di cicli moltiplicato per il periodo di quella frequenza. Ad esempio una finestra di 15 cicli avrà una larghezza a 1 kHz di 15 * (1/1000) = 0,015 s o 15 ms. La corrispondente frazione di ottava ha un effetto simile all'applicazione di uno smoothing della stessa frazione di ottava, tranne per il fatto che la finestra variabile esclude progressivamente una parte maggiore del suono che arriva tardi man mano che la frequenza aumenta, anziché limitarsi a calcolarne semplicememte la media. Questo assomiglia al modo in cui l'orecchio capta sempre più emette il suono diretto proveniente dall'altoparlante alle frequenze più alte.
Se è selezionata l'opzione Add frequency dependent window, questa viene applicata dopo aver prima applicato le finestre sinistra e destra selezionate. L'FDW (frequency dependent window) è centrata sul tempo di riferimento della finestra: per ottenere i migliori risultati, questa dovrebbe essere al picco dell'impulso.
Indice dei contenuti - Torna su



