Da REW Wiki.
|
|
| Riga 34: |
Riga 34: |
| | ===RTA=== | | ===RTA=== |
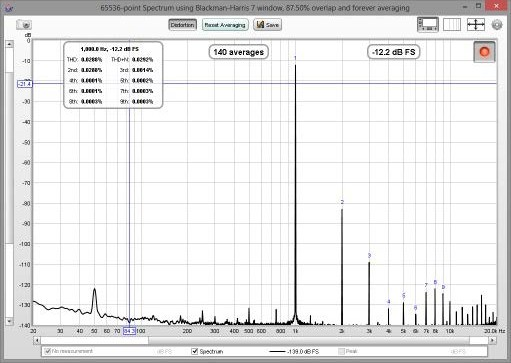
| | <div align="justify">Un modo comune per visualizzare lo spettro di un segnale di tempo, è l'utilizzo di un Real Time Analyser o RTA. L' RTA mostra un grafico delle ampiezze delle frequenze dei segnali che sta analizzando. Tuttavia, mentre la FFT produce segnali che sono a frequenze uniformemente distanziate, un RTA le raggruppa insieme in frazioni di ottava. Un'ottava, equivale ad un raddoppio della frequenza, così, l'intervallo tra 100Hz e 200Hz equivale ad un'ottava, così come l'intervallo tra 1kHz e 2kHz. L'intervallo di frequenza di una frazione di ottava, è maggiore della frequenza che si ottiene. Per una RTA a 1/3 di ottava, l'intervallo è di 4.6Hz a 20Hz, ma è di 4.6kHz a 20kHz. Per una RTA a 1/24 di ottava, gli intervalli sono 1/8 più larghi. All'interno dell'intervallo di una frazione di ottava, molti singoli valori FFT possono essere usati per produrre il singolo valore che l'RTA assegna a quella banda di frequenze. In basso, è visualizzata un'immagine dell'RTA di REW che mostra lo spettro di un tono a 1KHz e la sua distorsione armonica.</div> | | <div align="justify">Un modo comune per visualizzare lo spettro di un segnale di tempo, è l'utilizzo di un Real Time Analyser o RTA. L' RTA mostra un grafico delle ampiezze delle frequenze dei segnali che sta analizzando. Tuttavia, mentre la FFT produce segnali che sono a frequenze uniformemente distanziate, un RTA le raggruppa insieme in frazioni di ottava. Un'ottava, equivale ad un raddoppio della frequenza, così, l'intervallo tra 100Hz e 200Hz equivale ad un'ottava, così come l'intervallo tra 1kHz e 2kHz. L'intervallo di frequenza di una frazione di ottava, è maggiore della frequenza che si ottiene. Per una RTA a 1/3 di ottava, l'intervallo è di 4.6Hz a 20Hz, ma è di 4.6kHz a 20kHz. Per una RTA a 1/24 di ottava, gli intervalli sono 1/8 più larghi. All'interno dell'intervallo di una frazione di ottava, molti singoli valori FFT possono essere usati per produrre il singolo valore che l'RTA assegna a quella banda di frequenze. In basso, è visualizzata un'immagine dell'RTA di REW che mostra lo spettro di un tono a 1KHz e la sua distorsione armonica.</div> |
| | + | |
| | + | |
| | + | [[File:spettro.png | center]] |
| | + | |
| | + | |
| | + | ===Sistemi e Funzioni di Trasferimento=== |
| | + | |
| | + | <div align="justify">La visualizzazione di un segnale, ha la sua utilità, ma noi siamo interessati anche a quanto un apparato altera lo spettro dei segnali. Il modo in cui un sistema modifica lo spettro del segnale che lo attraversa, è chiamato Funzione di trasferimento. La funzione di trasferimento, ha due componenti: la Risposta in frequenza e la Risposta di fase. La risposta in frequenza, mostra la variazione delle ampiezze delle frequenze introdotte dal sistema, mentre la risposta di fase mostra parimenti la variazione della fase delle frequenze. Una descrizione completa del sistema, richiede entrambe le risposte. Sistemi molto differenti, possono avere la stessa risposta in frequenza, ma la loro differente risposta di fase, ci consente di distinguerli.</div><br> |
| | + | |
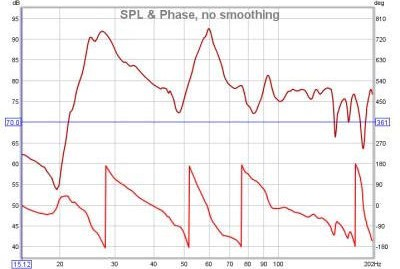
| | + | <div align="justify">Da notare che è importante non confondere la risposta in frequenza di un sistema con lo spettro di uscita del sistema. Ciò che lo spettro di un segnale ci mostra, è la sua composizione nei termini delle frequenze che contiene. La funzione di trasferimento della risposta in frequenza, ci dice come il sistema modifica lo spettro del segnale. Lo scopo di un software come REW è quello di misurare la funzione di trasferimento e i grafici di SPL & Fase, mostrano la funzione di trasferimento della frequenza e la risposta di fase. L’ampiezza della risposta in frequenza è mostrata come una traccia SPL. Sotto è possible vedere un grafico della risposta in frequenza (traccia superiore, asse di sinistra) e della risposta di fase (traccia inferiore, asse di destra), ricavate dalla misura di una stanza fino a una frequenza di 200Hz.</div> |
| | + | |
| | + | |
| | + | [[File:spl_e_fase.png | center]] |
| | + | |
| | + | |
| | + | ===La risposta all’impulso=== |
| | + | |
| | + | <div align="justify">La funzione di trasferimento, ci mostra attraverso le risposte di fase e di frequenza, come il sistema influisce sul segnale che lo attraversa. Essa caratterizza il sistema in quello che viene chiamato '''dominio della frequenza'''. Ma per quanto riguarda il segnale? Come possiamo descrivere come i singoli campioni del segnale vengono modificati dal sistema e il loro comportamento nel '''dominio del tempo'''? Il modo in cui il sistema modifica i campioni di un segnale, è detto '''risposta all’impulso'''. La ragione del nome sarà presto chiara. La risposta all’impulso (IR) è essa stessa un segnale composto da una serie di campioni. I segnali che vengono immessi nel sistema, si sovrappongono alla IR mentre lo attraversano, scorrendo campione per campione. Quando il segnale appare, il suo primo campione è allineato con il primo campione della risposta all’impulso. L’uscita del sistema per quel primo campione d’ingresso, è il valore del primo campione della IR, moltiplicato per il valore del primo campione del segnale: |
| | + | |
| | + | output[1] = input[1]*IR[1] |
| | + | |
| | + | Un campione di intervallo più tardi, l’ingresso ha 2 campioni sovrapposti con la IR. L’uscita per questo periodo di tempo è data dal secondo campione di tempo all’ingresso, moltiplicato per il primo campione della IR, più il primo campione di tempo all’ingresso, moltiplicato per il secondo campione della IR: |
| | + | |
| | + | output[2] = input[2]*IR[1] + input[1]*IR[2] |
| | + | |
| | + | Un altro campione di intervallo più tardi, l’ingresso ha 3 campioni sovrapposti con la IR. L’uscita sarà: |
| | + | output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3] |
| | + | <u>E così via per ogni successivo campione che appare. Il prodotto ottenuto dalla moltiplicazione dei campioni del segnale d’ingresso , con la IR, è chiamato '''convoluzione'''. Tipicamente, per la misurazione di una parte di un apparato, la risposta all’impulso è abbastanza di breve durata, molto meno di un secondo, mentre assume valori di un secondo o due, per la misura di una stanza di dimensioni casalinghe. Così eventualmente l’uscita ad ogni periodo di tempo, è data dalla lunghezza della IR, moltiplicata per la stessa lunghezza del segnale di ingresso, sommata a tutti i singoli prodotti fino ad ottenere l’uscita per quel periodo di tempo.</u></div> |
Versione delle 16:59, 15 apr 2016
Segnali e Misure
"Cosa significa tutta questa roba?"
Per dare un senso a tutte le misure che con REW si possono eseguire, è importante capirne il loro significato. Questo argomento fornisce una panoramica delle nozioni di base dei segnali e delle misure e spiega come sono generati i vari grafici all’interno di REW e come questi sono messi in relazione a quanto è stato misurato.
Segnali, Frequenza di campionamento e Risoluzione
La prima cosa, è comprendere cosa è un segnale, almeno nel contesto di esecuzione di una misura acustica. I segnali a cui noi siamo interessati, sono suoni registrati attraverso un microfono o attraverso un misuratore di SPL (Sound Pressure Level). La pressione sonora genera nel microfono / misuratore di SPL, un segnale elettrico che viene catturato dalla nostra scheda audio. La scheda audio effettua la misura del livello elettrico ai suoi ingressi. Ogni misura è indicata come campione. Quanto spesso I campioni vengono catturati, dipende dalla frequenza di campionamento. REW supporta frequenze di campionamento di 44.1kHz o 48kHz, che significa che la scheda audio cattura il segnale ai suoi ingressi, 44.100 o 48.000 volte al secondod. Tre secondi di un segnale campionato a 48kHz, significano una sequenza di 3 x 48.000 = 144.000 valori. La più alta frequenza che può essere catturata ad una data frequenza di campionamento, è pari alla metà di quest’ultima. Abbiamo quindi bisogno almeno di due campioni per ogni ciclo della frequenza da riprodurre. A 48kHz di campionamento, la massima frequenza che possiamo catturare è pari a 24kHz. Le frequenze più alte della metà della frequenza di campionamento, causerebbero aliasing, e apparirebbero più basse di quanto in realtà sono. Per esempio, un segnale a 25KHz, campionato a 48KHz, apparirebbe come un segnale a 23KHz. Per prevenire questo fenomeno, gli ingressi delle schede audio possiedono dei filtri anti-aliasing, che tentano di bloccare i segnali con frequenza più alta di quella che può essere catturata, ma essi non sono pienamente efficacy, così dobbiamo considerare il contenuto in frequenza del segnale che stiamo cercando di catturare.
La risoluzione delle misure della scheda audio, è tipicamente pari a 16 bit o 24 bit. La risoluzione a 16 bit, è la stessa utilizzata nei CD ed è supportata da REW. Avere 16 bit di risoluzione, significa che il range dei valori di una misura, è compreso tra -32768 e +32767 (numeri che possono essere rappresentati con 15 cifre binarie, più la 16^ cifra che indica il segno del numero). Anziché utilizzare direttamente i numeri della misura, è conveniente fare riferimento ad essi in termini di quanto si avvicinano al numero più grande e ciò rappresenta il Full Scale ed è abbreviato come FS. I valori full scale sono -32768 e +32767. Il più piccolo valore di misura diverso da zero, è 1, che come percentuale del full scale è 100 x (1/32768) o, approssimativamente lo 0.003% FS. Tutto ciò che è più piccolo di questo valore, è visto dalla scheda audio come zero. Il valore full scale, corrisponderà ad una certa tensione agli ingressi della scheda audio, che normalmente si aggira intorno a 1 Volt. Le schede audio che hanno una risoluzione maggiore (24 bit), generalmente hanno lo stessa tensione massima di ingresso (circa 1 Volt) ma possono usare una gamma maggiore di numeri per misurare la tensione di ingresso. Per una scheda audio a 24-bit, il numero di valori full scale varia da -8388608 a +8388607. Questo rappresenta ancora solo 1 Volt (tipicamente). Il valore più grande non è cambiato ma è cambiata la risoluzione che, per una scheda audio a 24-bit, equivale a misurare il più piccolo valore pari a 100 x (1/8388608) percentuale del full scale, cioè 0.000012% FS. Quindi, la maggior risoluzione offre benefici nella misura di segnali molto piccoli. Il valore full scale è spesso trattato come corrispondente al valore uno e tutto ciò che si trova sotto tale valore rispetto al full scale, è considerato come la corrispondente proporzione di uno. Così mezzo full scale sarà 0.5 e così via.
Clipping
Se il segnale è maggiore del valore full scale che la scheda audio è in grado di trattare, il valore della misura non potrà essere in ogni caso maggiore del valore full scale, qualsiasi cosa succeda all’ingresso. Quando il segnale è andato al di là del range che l’ingresso è in grado di misurare, si dice che che questo è clippato. Il clipping è visualizzato come una parte piatta della risposta. Se avviene all’ingresso della scheda audio, sarà a +100% FS o a -100% FS e REW vi avviserà, ma talvolta, il clipping avviene prima che il segnale raggiunga
la scheda audio (per esempio, nel preamplificatore microfonico, se è stato impostato un guadagno troppo elevato). In questo caso, la misura del valore, non arriverà mai al valore FS della scheda audio, ma il segnale sarà comunque clippato. Il clipping deve essere evitato durante la misura, perchè il segnale catturato, non rappresenta più ciò che realmente accade all’ingresso e che ha corrotto la misura.
Visualizzare i segnali
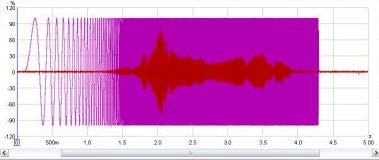
Un metodo per visualizzare i segnali, è quello di tracciarne i valori rispetto al tempo. Quando i valori dei segnali catturati vengono tracciati nel grafico dell’oscilloscopio di REW, essi vengono mostrati come % FS. Un segnale che raggiunge il 100% FS, è il più grande segnale che la scheda audio è in grado di catturare. Un esempio è mostrato qui sotto e visualizza un segnale di sweep generato da REW e (in rosso), la risultante catturata dal microfono.
Noi siamo generalmente interessati oltre che ai valori dei campioni, alle frequenze che compongono il segnale. La gamma di frequenze che compongono un segnale, è detta Spettro e possiamo calcolarle utilizzando la Fast Fourier Transform o FFT. La FFT elabora le ampiezze e le fasi di un set di onde cosinusoidali che, quando sommate tra loro, danno origine allo stesso insieme di valori di misura del segnale di tempo. L’ampiezza e le fasi di queste onde cosinusoidali, sono un modo differente di rappresentare il segnale di tempo in termini di frequenze che lo compongono, anziché utilizzarne i suoi singoli valori di misura. Le ampiezze, sono facili da comprendere. Una grande ampiezza del segnale, significa una grande onda cosinusoidale. Le fasi indicano invece il valore di partenza dell'onda cosinusoidale al tempo del primo campione, nella sequenza che è stata misurata. Una fase di 0 gradi, significa che il valore di partenza ha un'ampiezza che vale: "ampiezza x cos(0) = ampiezza. Una fase di 90 gradi, significa che il valore iniziale vale: "ampiezza x cos(90) = 0". Noi siamo spesso più interessati dai valori delle ampiezze che a quelli delle fasi, ma non dovremmo dimenticare queste ultime, poichè da sole, contengono la metà delle informazioni riguardo alla forma del segnale di tempo originale.
Quando, per calcolare lo spettro, facciamo uso della FFT, essa usa un pacchetto di frequenze che, uniformemente distanziate, partono dalla DC (frequenza zero) fino alla metà della frequenza di campionamento (il massimo che può essere correttamente rappresentato). La spaziatura, dipende dalla lunghezza del segnale che intendiamo analizzare con la FFT. I calcoli della FFT, sono molto più efficienti, quando le lunghezze dei segnali, sono potenze di 2, come 16k (16,384), 32k (32768) o 64k (65536). Per calcolare la FFT a 64k di un segnale che è campionato a 48kHz, abbiamo bisogno di 65536/48000 secondi di segnale, cioè 1.365s. Le frequenze, saranno spaziate di 24000/65536 = 0.366Hz. Se la FFT è stata generata da campioni a 16k, le frequenze sarebbero spaziate di 1.465Hz. Più le frequenze sono tra loro distanti, minore è la risoluzione in frequenza. Per una alta risoluzione in frequenza, dobbiamo analizzare i segnali per un lungo periodo di tempo.
RTA
Un modo comune per visualizzare lo spettro di un segnale di tempo, è l'utilizzo di un Real Time Analyser o RTA. L' RTA mostra un grafico delle ampiezze delle frequenze dei segnali che sta analizzando. Tuttavia, mentre la FFT produce segnali che sono a frequenze uniformemente distanziate, un RTA le raggruppa insieme in frazioni di ottava. Un'ottava, equivale ad un raddoppio della frequenza, così, l'intervallo tra 100Hz e 200Hz equivale ad un'ottava, così come l'intervallo tra 1kHz e 2kHz. L'intervallo di frequenza di una frazione di ottava, è maggiore della frequenza che si ottiene. Per una RTA a 1/3 di ottava, l'intervallo è di 4.6Hz a 20Hz, ma è di 4.6kHz a 20kHz. Per una RTA a 1/24 di ottava, gli intervalli sono 1/8 più larghi. All'interno dell'intervallo di una frazione di ottava, molti singoli valori FFT possono essere usati per produrre il singolo valore che l'RTA assegna a quella banda di frequenze. In basso, è visualizzata un'immagine dell'RTA di REW che mostra lo spettro di un tono a 1KHz e la sua distorsione armonica.
Sistemi e Funzioni di Trasferimento
La visualizzazione di un segnale, ha la sua utilità, ma noi siamo interessati anche a quanto un apparato altera lo spettro dei segnali. Il modo in cui un sistema modifica lo spettro del segnale che lo attraversa, è chiamato Funzione di trasferimento. La funzione di trasferimento, ha due componenti: la Risposta in frequenza e la Risposta di fase. La risposta in frequenza, mostra la variazione delle ampiezze delle frequenze introdotte dal sistema, mentre la risposta di fase mostra parimenti la variazione della fase delle frequenze. Una descrizione completa del sistema, richiede entrambe le risposte. Sistemi molto differenti, possono avere la stessa risposta in frequenza, ma la loro differente risposta di fase, ci consente di distinguerli.
Da notare che è importante non confondere la risposta in frequenza di un sistema con lo spettro di uscita del sistema. Ciò che lo spettro di un segnale ci mostra, è la sua composizione nei termini delle frequenze che contiene. La funzione di trasferimento della risposta in frequenza, ci dice come il sistema modifica lo spettro del segnale. Lo scopo di un software come REW è quello di misurare la funzione di trasferimento e i grafici di SPL & Fase, mostrano la funzione di trasferimento della frequenza e la risposta di fase. L’ampiezza della risposta in frequenza è mostrata come una traccia SPL. Sotto è possible vedere un grafico della risposta in frequenza (traccia superiore, asse di sinistra) e della risposta di fase (traccia inferiore, asse di destra), ricavate dalla misura di una stanza fino a una frequenza di 200Hz.
La risposta all’impulso
La funzione di trasferimento, ci mostra attraverso le risposte di fase e di frequenza, come il sistema influisce sul segnale che lo attraversa. Essa caratterizza il sistema in quello che viene chiamato
dominio della frequenza. Ma per quanto riguarda il segnale? Come possiamo descrivere come i singoli campioni del segnale vengono modificati dal sistema e il loro comportamento nel
dominio del tempo? Il modo in cui il sistema modifica i campioni di un segnale, è detto
risposta all’impulso. La ragione del nome sarà presto chiara. La risposta all’impulso (IR) è essa stessa un segnale composto da una serie di campioni. I segnali che vengono immessi nel sistema, si sovrappongono alla IR mentre lo attraversano, scorrendo campione per campione. Quando il segnale appare, il suo primo campione è allineato con il primo campione della risposta all’impulso. L’uscita del sistema per quel primo campione d’ingresso, è il valore del primo campione della IR, moltiplicato per il valore del primo campione del segnale:
output[1] = input[1]*IR[1]
Un campione di intervallo più tardi, l’ingresso ha 2 campioni sovrapposti con la IR. L’uscita per questo periodo di tempo è data dal secondo campione di tempo all’ingresso, moltiplicato per il primo campione della IR, più il primo campione di tempo all’ingresso, moltiplicato per il secondo campione della IR:
output[2] = input[2]*IR[1] + input[1]*IR[2]
Un altro campione di intervallo più tardi, l’ingresso ha 3 campioni sovrapposti con la IR. L’uscita sarà:
output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3]
E così via per ogni successivo campione che appare. Il prodotto ottenuto dalla moltiplicazione dei campioni del segnale d’ingresso , con la IR, è chiamato convoluzione. Tipicamente, per la misurazione di una parte di un apparato, la risposta all’impulso è abbastanza di breve durata, molto meno di un secondo, mentre assume valori di un secondo o due, per la misura di una stanza di dimensioni casalinghe. Così eventualmente l’uscita ad ogni periodo di tempo, è data dalla lunghezza della IR, moltiplicata per la stessa lunghezza del segnale di ingresso, sommata a tutti i singoli prodotti fino ad ottenere l’uscita per quel periodo di tempo.