Segnali e misure: differenze tra le versioni
(→Perchè è chiamata "risposta all’impulso"?) |
|||
| (108 versioni intermedie di uno stesso utente non sono mostrate) | |||
| Riga 1: | Riga 1: | ||
| − | ==Segnali e | + | ==<span style="color:#00007f";>Segnali e misure</span>== |
| − | ==="Cosa significa tutta questa roba?"=== | + | ===<span style="color:#4076c0; text-decoration: underline;">"Cosa significa tutta questa roba?"</span>=== |
| − | |||
| + | <div style="text-align:justify;">Per dare un senso a tutte le misure che con REW si possono eseguire, è importante capirne il loro significato. Questo argomento fornisce una panoramica delle nozioni di base dei segnali e delle misure e spiega come sono generati i vari grafici all’interno di REW e come questi sono messi in relazione a quanto è stato misurato.</div> | ||
| + | ---- | ||
| − | |||
| − | < | + | ===<span style="color:#4076c0; text-decoration: underline;">Segnali, Frequenza di campionamento e Risoluzione</span>=== |
| − | <div | + | <div style="text-align:justify;">La prima cosa da comprendere è cos'è un segnale, almeno nel contesto di esecuzione delle misure acustiche. I segnali a cui noi siamo interessati, sono suoni registrati attraverso un microfono o attraverso un fonometro. La pressione sonora catturata dal microfono / fonometro, genera dei segnali elettrici che vengono acquisiti dalla nostra interfaccia audio, che effettua al suo ingresso, la misurazione del livello elettrico. Ogni misurazione, è definita come '''campione'''. La frequenza con la quale i campioni vengono prelevati, dipende dalla '''frequenza di campionamento'''. REW supporta frequenze di campionamento di 44.1kHz o 48kHz, che sta ad indicare quante volte l'interfaccia audio cattura il segnale presente ai suoi ingressi: 44.100 o 48.000 volte al secondo. Tre secondi di un segnale campionato a 48kHz, significano una sequenza di 3 x 48.000 = 144.000 valori. La più alta frequenza che può essere catturata ad una data frequenza di campionamento, è pari alla metà della frequenza di campionamento stessa. Abbiamo quindi bisogno almeno di due campioni per ogni ciclo di frequenza di campionamento per poterla riprodurre. A 48kHz di campionamento, la massima frequenza che possiamo catturare è pari a 24kHz. Le frequenze che superano la metà della frequenza di campionamento, causerebbero '''aliasing''', e apparirebbero più basse di quanto in realtà sono. Per esempio, un segnale a 25KHz, campionato a 48KHz, apparirebbe come un segnale a 23KHz. Per prevenire questo fenomeno, gli ingressi delle interfacce audio posseggono dei filtri anti-aliasing, che tentano di bloccare i segnali con una frequenza più alta di quella massima catturabile, ma, non essendo pienamente efficaci, dobbiamo sempre considerare il contenuto in frequenza del segnale che stiamo cercando di catturare.</div> |
| − | = | + | <div style="text-align:justify;">La '''risoluzione''' delle misure delle interfacce audio, è tipicamente pari a 16 bit o 24 bit. La risoluzione a 16 bit, è la stessa utilizzata nei CD ed è supportata da REW. Avere 16 bit di risoluzione, significa che l'intervallo dei valori di una misura, è compreso tra -32768 e +32767 (numeri che possono essere rappresentati con 15 cifre binarie, più la 16^ cifra per memorizzare il segno del numero). Anziché utilizzare direttamente i numeri della misura, è conveniente fare riferimento ad essi in termini di quanto si avvicinano al numero più grande riferito al '''Fondo Scala''' (Full Scale) abbreviato come '''FS'''. I valori FS sono -32768 e +32767. Il più piccolo valore di misura diverso da zero, è 1, che, come percentuale del fondo scala, equivale a 100 x (1/32768) o, approssimativamente lo 0.003% FS. Tutto ciò che è più piccolo di questo valore, è visto dall'interfaccia audio come zero. Il valore di fondo scala, corrisponderà ad una certa tensione agli ingressi della scheda audio, che normalmente si aggira intorno a 1 Volt. Le schede audio che hanno una risoluzione maggiore (24 bit), generalmente accettano la stessa tensione massima (circa 1 Volt), ma possono usare una gamma maggiore di valori per misurare la tensione di ingresso. Per una scheda audio a 24-bit, il numero di valori riferito al FS, varia da -8388608 a +8388607. Questo, rappresenta ancora solo 1 Volt (tipicamente), e non è cambiato ma, data la risoluzione maggiore, il più piccolo valore che può essere rilevato, è pari a 100 x (1/8388608) percentuale del FS, cioè 0.000012% FS. Quindi, la maggior risoluzione offre benefici nella misura di segnali molto piccoli. Il valore di fondo scala è spesso trattato come corrispondente al valore uno e tutto ciò che si trova sotto tale valore rispetto al fondo scala, è considerato come la corrispondente proporzione di uno. Così mezzo fondo scala sarà 0.5 e così via.</div> |
| + | ---- | ||
| − | |||
| − | + | ===<span style="color:#4076c0; text-decoration: underline;">Clipping</span>=== | |
| + | <div style="text-align:justify;">Se il segnale è maggiore del valore di fondo scala, l'interfaccia | ||
| + | audio non sarà in grado di trattarlo. Il valore di misurazione, non potrà essere in ogni caso maggiore del valore FS, qualsiasi cosa succeda all’ingresso. Quando il segnale è andato al di là dell'intervallo che l’ingresso è in grado di misurare, si dice che è stato '''clippato''' (tagliato). Il clipping è visualizzato sui segnali di ingresso, come una parte piatta della risposta. Se avviene all’ingresso dell'interfaccia, sarà a +100% FS o a -100% FS e REW vi avviserà, ma talvolta, il clipping avviene prima che il segnale raggiunga la destinazione finale (per esempio, nel preamplificatore microfonico, se è stato impostato un guadagno troppo elevato). In questo caso, i valori di misurazione, potrebbero non arrivare mai al valore FS della scheda audio, ma il segnale sarà comunque tagliato. Il clipping deve essere evitato durante la misura, perchè il segnale catturato, non rappresenta più ciò che realmente sta accadendo all’ingresso e ciò altera la misura.</div> | ||
| + | ---- | ||
| − | |||
| − | <div | + | ===<span style="color:#4076c0; text-decoration: underline;">Visualizzare i segnali</span>=== |
| + | |||
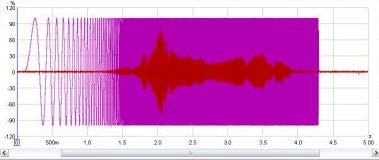
| + | <div style="text-align:justify;">Un metodo per osservare i segnali, è quello di tracciarne i valori rispetto al tempo. Quando i segnali catturati vengono tracciati nel grafico dell’'''oscilloscopio''' di REW, essi vengono mostrati come % '''FS'''. Un segnale che raggiunge il 100% FS, è il più grande segnale che l'interfaccia audio è in grado di catturare. Un esempio è mostrato qui sotto e visualizza un segnale di sweep generato da REW e (in rosso), la risultante catturata dal microfono.</div> | ||
| + | |||
[[File:grafico_oscilloscopio.png | center]] | [[File:grafico_oscilloscopio.png | center]] | ||
| − | |||
| − | <div | + | <div style="text-align:justify;">Noi siamo generalmente interessati a qualcosa di più dei semplici valori dei campioni. Potrebbero interessarci per esempio, le frequenze che compongono il segnale. La gamma di frequenze che compongono un segnale, è detta '''Spettro''' e possiamo calcolarle utilizzando la Fast Fourier Transform o '''FFT'''. La FFT elabora le ampiezze e le fasi di un set di onde cosinusoidali che, quando sommate tra loro, danno origine allo stesso insieme di valori di misura del segnale temporale. L’ampiezza e le fasi di queste onde cosinusoidali, sono un modo differente di rappresentare il segnale di tempo in termini di frequenze che lo compongono, anziché utilizzarne i suoi singoli valori di misurazione. Le ampiezze, sono facili da comprendere. Un'ampiezza maggiore, significa un'onda cosinusoidale più grande. Le fasi indicano invece il valore di partenza dell'onda cosinusoidale al tempo del primo campione, nella sequenza che è stata misurata. Una fase di 0 gradi, significa che il valore di partenza ha un'ampiezza che vale: "ampiezza x cos(0) = ampiezza. Una fase di 90 gradi, significa che il valore iniziale vale: "ampiezza x cos(90) = 0". Noi siamo più spesso interessati ai valori delle ampiezze che a quelli delle fasi, ma non dovremmo dimenticare queste ultime, poichè da sole, contengono la metà delle informazioni relative alla forma del segnale di tempo originale.</div> |
| + | <div style="text-align:justify;">Quando, per calcolare lo spettro, facciamo uso della FFT, essa usa un pacchetto di frequenze che sono uniformemente distanziate dalla DC (frequenza zero) fino alla metà della frequenza di campionamento (il massimo che può essere correttamente rappresentato). La spaziatura, dipende dalla lunghezza del segnale che intendiamo analizzare con la FFT. I calcoli della FFT, sono molto più efficienti, quando le lunghezze dei segnali sono potenze di 2, come 16k (16,384), 32k (32768) o 64k (65536). Per calcolare la FFT a 64k da un segnale che è campionato a 48kHz, abbiamo bisogno di 65536/48000 secondi di segnale, cioè 1.365s. Le frequenze, saranno distanziate di 24000/65536 = 0.366Hz. Se la FFT fosse generata da 16k campioni, le frequenze sarebbero distanziate di 1.465Hz. Minore è il numero di campioni utilizzati per generare la FFT, maggiore sarà la distanza tra le frequenze e minore sarà la risoluzione in frequenza. Per un'alta risoluzione in frequenza, dobbiamo analizzare lunghi periodi di tempo dei segnali.</div> | ||
| + | ---- | ||
| − | ===RTA (Real Time Analyzer)=== | + | |
| − | <div | + | ===<span style="color:#4076c0; text-decoration: underline;">RTA (Real Time Analyzer)</span>=== |
| + | |||
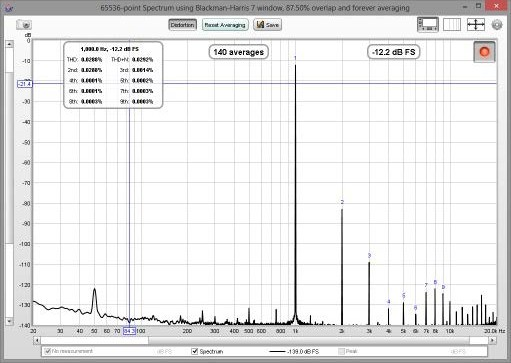
| + | <div style="text-align:justify;">Un modo comune per visualizzare lo spettro di un segnale, è l'utilizzo di un analizzatore in tempo reale o RTA (Real Time Analyser). L'RTA mostra un grafico delle ampiezze delle frequenze che compongono i segnali che si stanno analizzando. Tuttavia, mentre la FFT produce segnali che sono a frequenze uniformemente distanziate, un RTA li raggruppa insieme in frazioni di ottava. Un'ottava, equivale ad un raddoppio della frequenza, così, l'intervallo tra 100Hz e 200Hz equivale ad un'ottava, così come l'intervallo tra 1kHz e 2kHz. L'intervallo di frequenza di una frazione di ottava, è tanto maggiore quanto più alta diventa la frequenza che si ottiene. Per una RTA a 1/3 di ottava, l'intervallo è di circa 4.6Hz a 20Hz, ma è di 4.6kHz a 20kHz. Per una RTA a 1/24 di ottava, gli intervalli sono larghi 1/8. All'interno dell'intervallo di una frazione di ottava, possono essere utilizzati molti singoli valori FFT per produrre il singolo valore che l'RTA assegna a quella banda di frequenze. In basso, è visualizzata un'immagine dell'RTA di REW che mostra lo spettro di un tono a 1KHz e le sue distorsioni armoniche.</div> | ||
[[File:spettro.png | center]] | [[File:spettro.png | center]] | ||
| + | ---- | ||
| − | |||
| − | < | + | ===<span style="color:#4076c0; text-decoration: underline;">Sistemi e Funzioni di Trasferimento</span>=== |
| − | <div align="justify">Da notare che è importante non confondere la risposta in frequenza di un sistema con lo spettro di uscita del sistema. Ciò che lo spettro di un segnale ci mostra, è la sua composizione nei termini delle frequenze che contiene. La | + | <div style="text-align:justify;">La visualizzazione dello spettro di un segnale, ha la sua utilità, ma noi siamo interessati anche a quanto un apparato ''altera'' lo spettro dei segnali. Il modo in cui un sistema modifica lo spettro dei segnali che lo attraversano, è chiamato '''Funzione di Trasferimento''' del sistema. La funzione di trasferimento, ha due componenti: la '''Risposta in Frequenza''' e la '''Risposta di Fase'''. La risposta in frequenza, mostra come le |
| + | ampiezze delle frequenze vengono modificate dal sistema, mentre la risposta di fase mostra parimenti la variazione della fase delle stesse. Una descrizione completa del sistema, richiede entrambe le risposte. Sistemi molto differenti, possono avere la stessa risposta in frequenza, ma la loro differente risposta di fase sarà la caratteristica che permetterà di distinguerli.</div><br> | ||
| + | |||
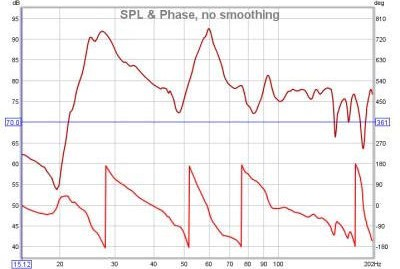
| + | <div style="text-align:justify;">Da notare che è importante non confondere la risposta in frequenza di un sistema con lo spettro di uscita del sistema. Ciò che lo spettro di un segnale ci mostra, è la sua composizione nei termini delle frequenze che contiene. La risposta in frequenza della funzione di trasferimento, ci dice come il sistema ''modifica'' lo spettro del segnale. Lo scopo di un software di misura come REW, è quello di misurare le funzioni di trasferimento e i grafici di '''SPL & Fase''', mostrano la frequenza della funzione di trasferimento e la risposta di fase. L’ampiezza della risposta in frequenza è mostrata come una traccia SPL. Sotto è possibile vedere un grafico della risposta in frequenza (traccia superiore, asse di sinistra) e della risposta di fase (traccia inferiore, asse di destra), ricavate da una misura ambientale che mostra l'intervallo fino a una frequenza di 200Hz.</div> | ||
[[File:spl_e_fase.png | center]] | [[File:spl_e_fase.png | center]] | ||
| + | ---- | ||
| − | ===La risposta all’impulso=== | + | ===<span style="color:#4076c0; text-decoration: underline;">La risposta all’impulso</span>=== |
| − | <div | + | <div style="text-align:justify;">La funzione di trasferimento, ci mostra attraverso le risposte di fase e di frequenza, come il sistema influenza lo spettro dei segnali che lo attraversano. Essa caratterizza il sistema in quello che viene chiamato '''dominio della frequenza'''. Ma per quanto riguarda il segnale stesso? In che modo possiamo descrivere come i singoli campioni del segnale vengono modificati dal sistema e il loro comportamento nel '''dominio del tempo'''? Il modo in cui un sistema modifica i campioni di un segnale, è detto '''risposta all’impulso'''. La ragione del nome sarà presto chiara. La risposta all’impulso (IR) è essa stessa un segnale composto da una serie di campioni. I segnali che vengono immessi nel sistema, si sovrappongono alla IR mentre lo attraversano, scorrendo su di esso, campione dopo campione. Quando il segnale appare per la prima volta, il suo primo campione sarà allineato con il primo campione della risposta all’impulso. L’uscita del sistema per quel primo campione d’ingresso, sarà il valore del primo campione della IR, moltiplicato per il primo valore del campione del segnale: |
output[1] = input[1]*IR[1] | output[1] = input[1]*IR[1] | ||
| − | Un | + | Un intervallo di campionamento più tardi, l’ingresso presenterà la sovrapposizione di 2 campioni con la IR. L’uscita per questo periodo di tempo sarà data dal secondo campione di ingresso, moltiplicato per il primo campione della IR, più il primo campione di ingresso, moltiplicato per il secondo campione della IR: |
output[2] = input[2]*IR[1] + input[1]*IR[2] | output[2] = input[2]*IR[1] + input[1]*IR[2] | ||
| − | Un altro | + | Un altro intervallo di campionamento più tardi, l’ingresso avrà 3 campioni sovrapposti con la IR. L’uscita sarà: |
output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3] | output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3] | ||
| − | + | E così via per ogni successivo campione che appare. Il prodotto ottenuto dalla moltiplicazione dei campioni del segnale d’ingresso , con i campioni della IR, è chiamato '''convoluzione'''. Tipicamente, per la misurazione di un apparto, la risposta all’impulso ha una durata piuttosto breve, molto meno di un secondo, mentre assume valori di un secondo o due, per la misura di una stanza domestica di medie dimensioni.</div> | |
| + | ---- | ||
| − | ===Perchè è chiamata "risposta all’impulso"?=== | + | ===<span style="color:#4076c0; text-decoration: underline;">Perchè è chiamata "risposta all’impulso"?</span>=== |
| − | <div | + | <div style="text-align:justify;">Che risultato otterremmo, se il segnale d’ingresso fosse costituito da un singolo campione a fondo scala, al quale abbiamo assegnato un valore pari a uno, seguito da valori pari a zero per tutti gli altri campioni? Il campione iniziale risultante sarebbe: |
output[1] = input[1]*IR[1] = '''IR[1]''' | output[1] = input[1]*IR[1] = '''IR[1]''' | ||
| − | Il successivo campione sarebbe: | + | Il successivo campione di uscita sarebbe: |
output[2] = input[2]*IR[1] + input[1]*IR[2] = 0*IR[1] + 1*IR[2] = '''IR[2]''' | output[2] = input[2]*IR[1] + input[1]*IR[2] = 0*IR[1] + 1*IR[2] = '''IR[2]''' | ||
| Riga 77: | Riga 90: | ||
output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3] = 0*IR[1] + 0*IR[2] + 1*IR[3] = '''IR[3]''' | output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3] = 0*IR[1] + 0*IR[2] + 1*IR[3] = '''IR[3]''' | ||
| − | e così via. L’uscita | + | e così via. L’uscita consisterebbe in ciascun campione della IR a turno. Un segnale di ingresso costituito da un singolo campione a fondo scala, seguito da zeri, è chiamato '''impulso'''. Quindi, quando l'uscita del sistema, è alimentata da un simile segnale, ciò viene definita ''risposta all’impulso''.</div> |
| + | ---- | ||
| + | |||
| + | |||
| + | ===<span style="color:#4076c0; text-decoration: underline;">Relazione tra la Funzione di Trasferimento e la Risposta all’Impulso</span>=== | ||
| + | |||
| + | <div align="justify>Poichè la funzione di trasferimento e la risposta all’impulso sono entrambe descrizioni dello stesso sistema, potremmo ragionevolmente supporre che siano tra loro correlate e lo sono. La funzione di trasferimento è la FFT della risposta all’impulso, e la risposta all’impulso è la FFT inversa della funzione di trasferimento. Entrambe sono visioni dello stesso sistema, una nel dominio della frequenza, e l’altra nel dominio del tempo. La funzione di trasferimento, è semplicemente lo spettro della risposta all’impulso.</div> | ||
| + | ---- | ||
| + | |||
| + | |||
| + | ===<span style="color:#4076c0; text-decoration: underline;">Visualizzare la risposta all’impulso</span>=== | ||
| + | |||
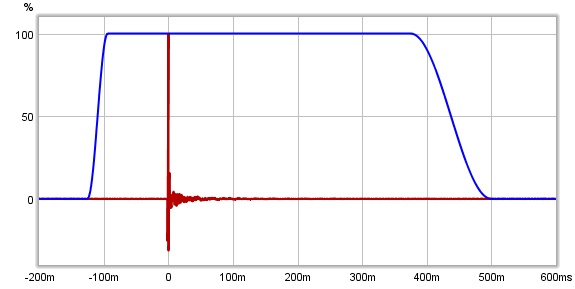
| + | <div style="text-align:justify;">Il grafico di REW, mostra la risposta all’impulso. I valori sono espressi in % FS o in '''dB FS'''. La scala in dB, è utile per visualizzare una dinamica più ampia del segnale e, anzichè tracciare i valori direttamente, traccia il log in base 10 dei valori, moltiplicati per 20. La parte superiore del grafico in dB, è a 0dBFS, che corrisponde al 100% FS. Ad un livello del 50% FS, corrisponde 20*log(0.5) = -6dBFS. Il 10% FS equivale a 20*log(0.1) = -20dBFS. La scala in dBFS, è utile per vedere come si comportano i livelli più bassi dell’impulso e dove sparisce al di sotto del livello di rumore della misura. | ||
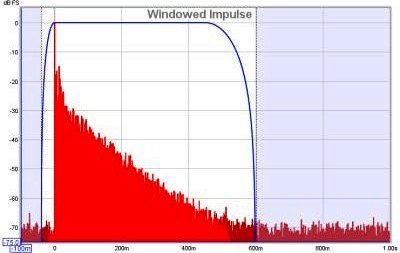
| + | Le immagini qui sotto mostrano, la prima, la risposta all’impulso con l’asse delle Y impostato a % FS, e la seconda invece, mostra la stessa risposta utilizzando i dBFS. Nella seconda immagine possiamo vedere come l’impulso impieghi più tempo a decadere nel rumore di fondo, di quanto sembri invece dal grafico impostato in %FS.</div> | ||
| + | |||
| + | |||
| + | [[File:Impulseplot.jpg|center|impulso]]<br>[[File:Impulso_finestrato.png|center|impulso finestrato]] | ||
| + | ---- | ||
| + | |||
| + | ===<span style="color:#4076c0; text-decoration: underline;">Finestrare la Risposta all’Impulso</span>=== | ||
| + | |||
| + | <div style="text-align:justify;">Supponiamo di voler eseguire una misura su un dispositivo che potrebbe essere un altoparlante, ma in acustica, il sistema che stiamo misurando, comprende altre variabili che intervengono nel percorso tra il segnale generato per la misurazione e il segnale raccolto per l’analisi. Queste variabili, includono gli amplificatori, il microfono, l'interfaccia audio e soprattutto, la stanza stessa. Quindi il sistema nel suo complesso comprende tutti questi elementi e, per poterci concentrare solo su uno di essi, dovremo conoscere un modo per rimuovere l’influenza di tutte quelle parti alle quali non siamo interessati. La risposta dell'interfaccia audio, può essere calibrata misurandola separatamente, così come la risposta del microfono, mentre la rimozione degli effetti della stanza è molto più difficoltosa. Potrebbe essere proprio questa ciò che a noi interessa, specialmente se stiamo studiando ciò che sentiamo nella nostra posizione di ascolto ma, se cerchiamo di isolare le prestazioni di un altoparlante, il contributo della stanza potrebbe oscurare i dettagli che questo è in grado di fornire.<br> | ||
| + | Il viaggio del suono che raggiunge il microfono attraverso un percorso diretto dall’altoparlante, oltre ad essere il più breve, è quello che impiega il minor tempo. L’altoparlante però, irradia il suono anche in altre direzioni che lo fanno rimbalzare sulle varie superfici della stanza. Queste riflessioni, compiendo quindi un tragitto maggiore prima di raggiungere il microfono, impiegano un tempo maggiore prima di arrivare a destinazione. Nel caso di un impulso, questo arriverà prima delle riflessioni, che arriveranno invece ritardate. Questo ritardo, è determinato dal maggior tempo necessario al suono, a compiere un percorso maggiore. Minore è il ritardo, minore è il tempo impiegato dal suono per raggiungere la superficie più vicina (se, per esempio, la superficie più vicina fosse situata a 1 m. di distanza, il suono riflesso raggiungerebbe il microfono circa 3 ms più tardi rispetto al suono diretto proveniente dall’altoparlante).<br> | ||
| + | Se dovessimo analizzare solo i primi pochi ms della risposta all’impulso, vedremmo la parte corrispondente all’arrivo iniziale, che proviene direttamente dall’altoparlante, senza alcun | ||
| + | contributo della stanza. Analizzando in questo modo, una piccola porzione della risposta all’impulso, eseguiremmo una '''finestratura''' della risposta (nelle immagini della risposta all’impulso, pochi righe sopra, la traccia blu mostra la finestra). Calcolando una FFT per quella porzione finestrata della IR (risposta all’impulso), potremmo vedere la funzione di trasferimento per quell’istante che corrisponderebbe alla funzione di trasferimento del solo altoparlante. Tuttavia, c’è uno svantaggio. Infatti, se prendiamo la FFT di un segnale breve, potremmo vedere la risposta solamente fino a un limite che dipende dalla durata del segnale in esame. Se avessimo un intero secondo di segnale da analizzare, potremmo ottenere una risposta in frequenza che scende fino a 1Hz mentre, se avessimo un segnale che dura solo 1/10 di secondo, la risposta scenderebbe fino a 10Hz. Generalmente, se la lunghezza del segnale da analizzare, vale T secondi, la frequenza più bassa vale 1/T. Così se la nostra finestra durasse 3ms, la risposta in frequenza scenderebbe solo fino a 1/0.003 = 333Hz. Così, per vedere le risposte a bassa frequenza senza le influenze ambientali, la superficie più vicina deve essere la più lontana possibile.. Per regolare le impostazioni della finestra in REW, cliccare sul pulsante '''IR Windows'''. Per impostazione predefinita, REW usa impostazioni della finestra che includono più di 0.5s della risposta all’impulso, in modo che gli effetti della stanza siano visibili.</div> | ||
| + | ---- | ||
| + | |||
| + | |||
| + | ===<span style="color:#4076c0; text-decoration: underline;">Waterfall (grafico a cascata)</span>=== | ||
| + | |||
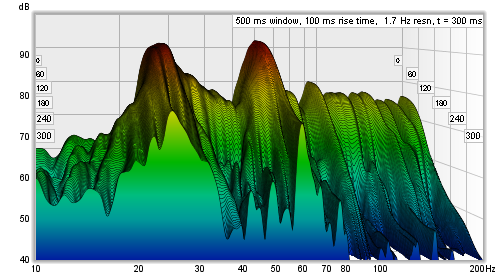
| + | <div style="text-align:justify;">I grafici relativi alla SPL, alla Fase e all’Impulso, sono i più utili per lo studio della funzione di trasferimento che abbiamo catturato, ma esiste un altro grafico che ci fornisce utili informazioni su come la stanza reagisce rispetto ai suoni in essa riprodotti. Tale grafico è detto '''Waterfall''', e mostra come lo spettro di una sezione della risposta all’impulso cambia, con il passare del tempo. Esso è ottenuto, finestrando una parte iniziale della risposta, tipicamente qualche centinaia di ms quando si osservano le risposte della stanza, e calcolando la FFT di quella sezione finestrata. La FFT, produce la prima fetta del grafico a cascata. Spostiamo quindi leggermente la finestra lungo la risposta all’impulso, e calcoliamo un'altra FFT per ottenere la seconda fetta del grafico. Spostiamo ancora leggermente la finestra, per ottenere la terza fetta, poi la quarta e così via. Man mano che ci muoviamo in avanti sul grafico a cascata, iniziamo a perdere il contributo iniziale dato dall’altoparlante e iniziamo a vedere sempre di più, solo il contributo dato dalla stanza. La risposta di quest’ultima, è più forte alle frequenze in cui sono presenti delle '''risonanze modali''', ovvero a frequenze alle quali il suono rimbalza avanti e indietro tra le pareti della stanza, rinforzandosi e producendo toni stabili con un lento decadimento. Queste frequenze sono mostrate nel grafico come creste. Più le creste sono alte, peggiori sono le risonanze modali, con lunghi tempi di decadimento.</div> | ||
| + | |||
| + | [[File:waterfall.png]] | ||
| + | |||
| + | <div style="text-align:justify;">Questa è stata una veloce introduzione ai concetti che stanno alla base della teoria dei segnali e delle misure. Se siete riusciti a restare incollati fino alla fine, ben fatto! Ora avete le informazioni necessarie per comprendere meglio come REW [[Iniziare con REW#Come REW esegue le misure|esegue le misure]].</div> | ||
| + | ---- | ||
| + | |||
| + | |||
| + | [[Indice dei contenuti]] - [[#top|Torna su]] | ||
Versione attuale delle 13:22, 18 set 2023
Indice
- 1 Segnali e misure
- 1.1 "Cosa significa tutta questa roba?"
- 1.2 Segnali, Frequenza di campionamento e Risoluzione
- 1.3 Clipping
- 1.4 Visualizzare i segnali
- 1.5 RTA (Real Time Analyzer)
- 1.6 Sistemi e Funzioni di Trasferimento
- 1.7 La risposta all’impulso
- 1.8 Perchè è chiamata "risposta all’impulso"?
- 1.9 Relazione tra la Funzione di Trasferimento e la Risposta all’Impulso
- 1.10 Visualizzare la risposta all’impulso
- 1.11 Finestrare la Risposta all’Impulso
- 1.12 Waterfall (grafico a cascata)
Segnali e misure
"Cosa significa tutta questa roba?"
Segnali, Frequenza di campionamento e Risoluzione
Clipping
Visualizzare i segnali
RTA (Real Time Analyzer)
Sistemi e Funzioni di Trasferimento
La risposta all’impulso
output[1] = input[1]*IR[1]
Un intervallo di campionamento più tardi, l’ingresso presenterà la sovrapposizione di 2 campioni con la IR. L’uscita per questo periodo di tempo sarà data dal secondo campione di ingresso, moltiplicato per il primo campione della IR, più il primo campione di ingresso, moltiplicato per il secondo campione della IR:
output[2] = input[2]*IR[1] + input[1]*IR[2]
Un altro intervallo di campionamento più tardi, l’ingresso avrà 3 campioni sovrapposti con la IR. L’uscita sarà: output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3]
E così via per ogni successivo campione che appare. Il prodotto ottenuto dalla moltiplicazione dei campioni del segnale d’ingresso , con i campioni della IR, è chiamato convoluzione. Tipicamente, per la misurazione di un apparto, la risposta all’impulso ha una durata piuttosto breve, molto meno di un secondo, mentre assume valori di un secondo o due, per la misura di una stanza domestica di medie dimensioni.
Perchè è chiamata "risposta all’impulso"?
output[1] = input[1]*IR[1] = IR[1]
Il successivo campione di uscita sarebbe:
output[2] = input[2]*IR[1] + input[1]*IR[2] = 0*IR[1] + 1*IR[2] = IR[2]
Il terzo campione sarebbe:
output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3] = 0*IR[1] + 0*IR[2] + 1*IR[3] = IR[3]
e così via. L’uscita consisterebbe in ciascun campione della IR a turno. Un segnale di ingresso costituito da un singolo campione a fondo scala, seguito da zeri, è chiamato impulso. Quindi, quando l'uscita del sistema, è alimentata da un simile segnale, ciò viene definita risposta all’impulso.
Relazione tra la Funzione di Trasferimento e la Risposta all’Impulso
Visualizzare la risposta all’impulso
Finestrare la Risposta all’Impulso
Il viaggio del suono che raggiunge il microfono attraverso un percorso diretto dall’altoparlante, oltre ad essere il più breve, è quello che impiega il minor tempo. L’altoparlante però, irradia il suono anche in altre direzioni che lo fanno rimbalzare sulle varie superfici della stanza. Queste riflessioni, compiendo quindi un tragitto maggiore prima di raggiungere il microfono, impiegano un tempo maggiore prima di arrivare a destinazione. Nel caso di un impulso, questo arriverà prima delle riflessioni, che arriveranno invece ritardate. Questo ritardo, è determinato dal maggior tempo necessario al suono, a compiere un percorso maggiore. Minore è il ritardo, minore è il tempo impiegato dal suono per raggiungere la superficie più vicina (se, per esempio, la superficie più vicina fosse situata a 1 m. di distanza, il suono riflesso raggiungerebbe il microfono circa 3 ms più tardi rispetto al suono diretto proveniente dall’altoparlante).
Se dovessimo analizzare solo i primi pochi ms della risposta all’impulso, vedremmo la parte corrispondente all’arrivo iniziale, che proviene direttamente dall’altoparlante, senza alcun