Grafico del decadimento dell'RT60: differenze tra le versioni
(→Analisi RT60) |
|||
| (81 versioni intermedie di uno stesso utente non sono mostrate) | |||
| Riga 1: | Riga 1: | ||
| − | ===<span style="color:# | + | ===<span style="color:#4076c0; text-decoration: underline;">Grafico del decadimento dell'RT60</span>=== |
| − | |||
| − | |||
| + | <div style="text-align:justify;">Il grafico di REW, relativo al decadimento dell'RT60, fornisce un modo per esaminare il comportamento del tempo di riverbero a risoluzioni di frequenza molto più elevate e con frazioni di ottava molto più strette di quanto sia normalmente possibile, anche a basse frequenze, grazie ad un approccio nel dominio della frequenza.</div> | ||
| − | |||
| + | [[File:Rt60model.jpg]] | ||
| + | ---- | ||
| − | + | ===<span style="color:#4076c0; text-decoration: underline;">Stima dell'RT60 nel dominio della frequenza</span>=== | |
| − | |||
| − | + | <div style="text-align:justify;">Il grafico di REW, relativo al decadimento dell'RT60, adotta per la stima di quest'ultimo, un approccio nel dominio della frequenza piuttosto che il più consueto approccio nel dominio del tempo.</div> | |
| − | <div align="justify">La | + | :*[[#Stima classica dell'RT60|Stima classica dell'RT60]] |
| − | Le impostazioni vengono | + | |
| + | :*[[#Un approccio nel dominio della frequenza alla stima dell'RT60|Un approccio nel dominio della frequenza alla stima dell'RT60]] | ||
| + | |||
| + | :*[[#Confronto di selettività|Confronto di selettività]] | ||
| + | |||
| + | :*[[#Confronto di precisione|Confronto di precisione]] | ||
| + | |||
| + | :*[[#Implementazione|Implementazione]] | ||
| + | |||
| + | ===<span style="color:#4076c0;">'''''Stima classica dell'RT60'''''</span>=== | ||
| + | <div style="text-align:justify;">I tempi di riverbero vengono solitamente determinati mediante l'elaborazione effettuata nel dominio del tempo. I diversi valori dell'RT60, vengono stimati calcolando la pendenza dell'integrale di Schroeder, che è un grafico dell'energia (valori al quadrato) della risposta all'impulso integrata al contrario (sommata partendo dalla fine e muovendosi a ritroso). Le diverse misure relative all'RT60 (ad esempio T20, T30, Topt di REW) vengono quindi derivate calcolando la linea di adattamento migliore all'integrale di Schroeder su diversi intervalli. Ci sono però alcune limitazioni a questo approccio, tra cui il rumore di fondo della misurazione che influenza la forma dell'integrale di Schroeder, facendolo curvare. Per ridurre tale effetto, vengono adottate varie misure stimando il livello del rumore di fondo e alterando il punto in cui inizia l'integrazione e i valori iniziali che questa utilizza. Inoltre, i filtri a bande d'ottava, presentano ritardi di gruppo che possono influenzare i tempi di riverbero calcolati, soprattutto alle basse frequenze, oltre a possedere solitamente una scarsa discriminazione di frequenza, poiché il loro ordine è generalmente basso (tipicamente il 6° ordine), per evitare di esasperare il problema del ritardo di gruppo. Di conseguenza, forti risonanze hanno un effetto di mascheramento sulle regioni vicine della risposta.</div><br> | ||
| + | ===<span style="color:#4076c0;">'''''Un approccio nel dominio della frequenza alla stima dell'RT60'''''</span>=== | ||
| + | <div style="text-align:justify;">I tempi di riverbero possono anche essere stimati attraverso l'elaborazione effettuata nel dominio della frequenza, esaminando i decadimenti delle sezioni di un insieme di grafici della trasformata di Fourier a tempo breve (STFT). Questi sono comunemente usati per produrre grafici a cascata o spettrogrammi. Le fette di una serie STFT possono essere filtrate in banda d'ottava nel dominio della frequenza utilizzando filtri brick wall senza nessun ritardo di gruppo associato nel dominio del tempo. La discriminazione di frequenza è quindi determinata dalle caratteristiche della finestra utilizzata per l'STFT, il cui fattore decisivo generalmente è determinato dalla larghezza e dalla forma del lato sinistro della finestra (noto anche come tempo di salita della finestra). L'elaborazione nel dominio della frequenza rende perciò semplice la presentazione dei risultati utilizzando dei filtri a banda d'ottava molto più stretti, consentendo quindi di distinguere le singole risonanze senza alcun impatto negativo sulla stima del tempo di riverbero.<br> | ||
| + | L'integrale di Schroeder non è applicabile all'elaborazione effettuata nel dominio della frequenza. Le porzioni STFT catturano i decadimenti del riverbero e il rumore e i tempi di riverbero possono essere stimati adattando una funzione esponenziale del decadimento più il rumore, alla serie di dati formata dai valori delle porzioni in ogni intervallo di tempo. Il processo di adattamento deve tenere conto dell'effetto della finestra di sinistra sulla serie di dati, dove la sua larghezza è maggiore dell'intervallo delle sezioni. Inoltre, deve anche essere tollerante nei confronti della natura non monotona dei dati di decadimento.<br> | ||
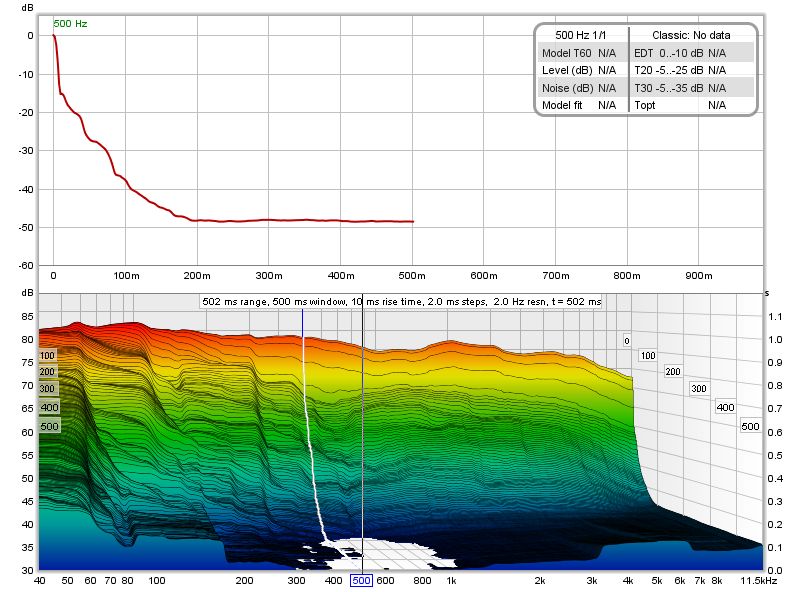
| + | Ecco un esempio di un grafico del decadimento dell'RT60, dopo aver generato i dati STFT (premendo il pulsante '''Generate''' nell'angolo in basso a sinistra nella parte inferiore del grafico), ma prima di calcolare il modello RT60. Il pannello superiore mostra la curva di decadimento riferita alla posizione del cursore nel grafico inferiore.</div> | ||
| + | |||
| + | |||
| + | [[File:Rt60decay.jpg]] | ||
| + | |||
| + | |||
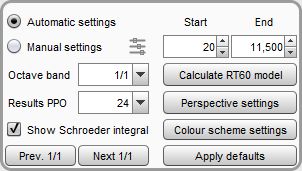
| + | Il pannello di controllo nel grafico inferiore è dotato di un pulsante per calcolare il modello dell'RT60. | ||
| + | |||
| + | |||
| + | [[File:Rt60decaycontrols.jpg]] | ||
| + | |||
| + | |||
| + | <div style="text-align:justify;">Sul lato sinistro del pannello sono collocati i controlli per i dati STFT. Quando è selezionato '''Automatic''', REW determinerà il tempo di salita, la larghezza della finestra e l'intervallo di tempo da utilizzare per il grafico STFT. L'opzione '''Manual''' consentirà di modificare tali impostazioni utilizzando il pulsante a destra della selezione Manuale. '''Octave band''', determina la larghezza del filtro a banda d'ottava applicato ai dati STFT, mentre '''Results PPO''', determina la risoluzione in frequenza alla quale REW calcolerà il modello (fino a 96 PPO). L'opzione '''Show Schroeder integral''', consente di mostrare il risultato dell'integrale di Schroeder relativo al calcolo dell'RT60 classico più vicino, accanto al profilo di decadimento. I pulsanti '''Prev. 1/1''' e '''Next 1/1''' spostano il cursore sulla frequenza centrale di 1 ottava precedente o successiva.</div><br> | ||
| + | <div style="text-align:justify;">Sul lato destro del pannello sono presenti i selettori che determinano l'intervallo di frequenza sul quale verrà calcolato l'adattamento del modello e il pulsante '''Calculate RT60 model''', che esegue il calcolo. Il pulsante '''Perspective settings''', apre una finestra di dialogo per controllare la presentazione dei dati STFT mentre il pulsante '''Colour scheme settings''', apre una finestra di dialogo per controllare la combinazione di colori.</div><br> | ||
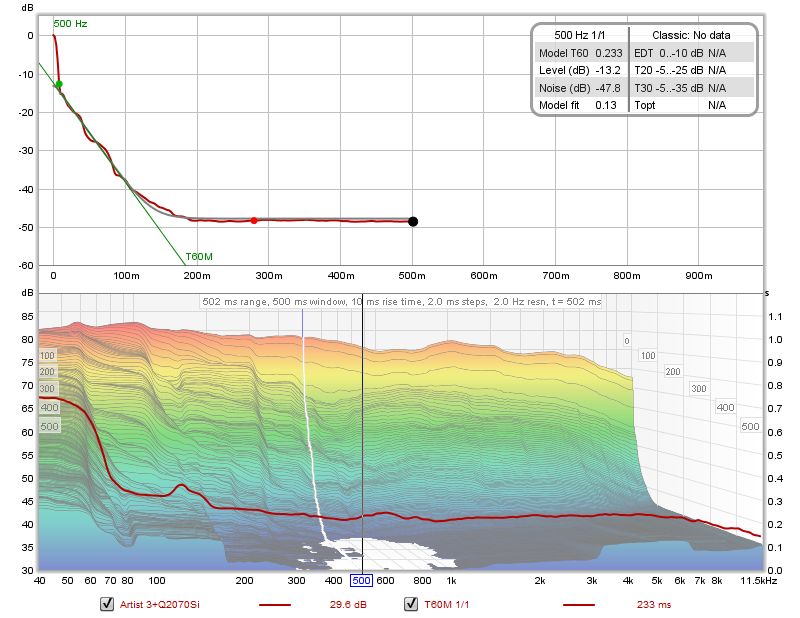
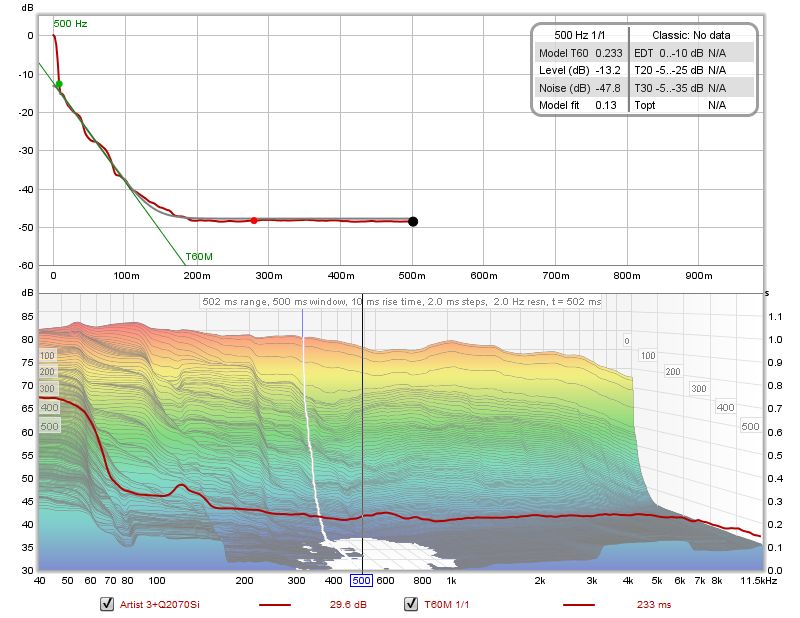
| + | <div style="text-align:justify;">Dopo che per ciascuna frequenza il modello è stato calcolato, il risultato (T60M) apparirà come sovrapposizione sui dati STFT, utilizzando un asse temporale sul lato destro del grafico. Questo potrà essere mostrato o nascosto selezionando o deselezionando la traccia T60M nell'apposita legenda. Nella parte superiore il risultato del modello sarà mostrato come una curva grigia, con una linea di regressione corrispondente al valore RT60 calcolato, mostrata in blu. Il pannello dati mostrerà il tempo T60, il livello iniziale della curva del modello, il livello di rumore e l'errore di adattamento del modello (minore è il valore, migliore è l'adattamento). Sulla curva di decadimento verranno mostrati tre punti. Il verde e il rosso indicano l'inizio e la fine dell'intervallo utilizzato per l'adattamento mentre il nero indica il punto oltre il quale REW considera i dati non validi.</div> | ||
| + | |||
| + | |||
| + | [[File:Rt60model (1).jpg]] | ||
| + | |||
| + | |||
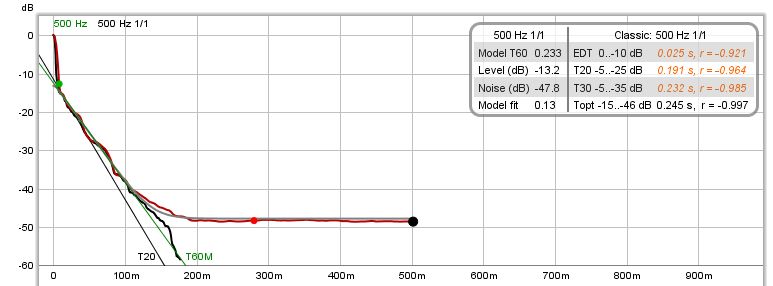
| + | <div style="text-align:justify;">Se per la misurazione vengono generati i risultati dell'RT60 classici (dal grafico RT60), tali valori verranno visualizzati insieme all'integrale di Schroeder e alla sua linea di regressione, se è stata selezionata l'opzione per la loro visualizzazione.</div> | ||
| + | |||
| + | |||
| + | [[File:Rt60modelwithclassic.jpg]] | ||
| + | |||
| + | |||
| + | <div style="text-align:justify;">In questo esempio, il valore classico T20 RT60 è inferiore al valore del modello. Ciò è comune nelle risposte che presentano decadimenti precoci e netti, come potrebbe accadere nel caso degli spazi fortemente trattati. Il punto a -5 dB sull'integrale di Schroeder (che è il punto di partenza per i valori T20 e T30), è ancora all'interno del decadimento iniziale, causando quindi una distorsione dei risultati.<br><br> | ||
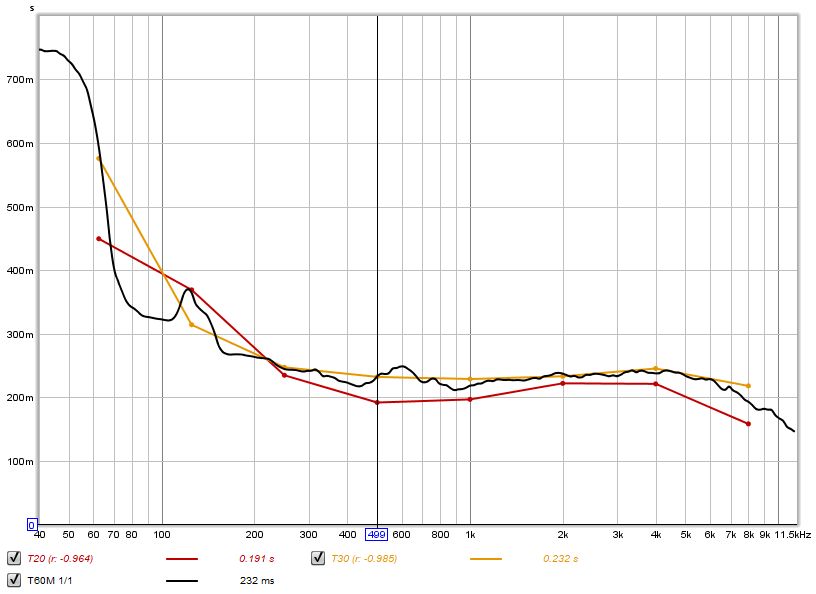
| + | Dopo che è stato effettuato il calcolo del modello, il risultato può essere visualizzato anche sul grafico RT60, consentendone un facile confronto con le misure classiche.</div> | ||
| + | |||
| + | |||
| + | [[File:Rt60classic.jpg]] | ||
| + | ---- | ||
| + | |||
| + | |||
| + | ===<span style="color:#4076c0;">'''''Confronto di selettività'''''</span>=== | ||
| + | |||
| + | |||
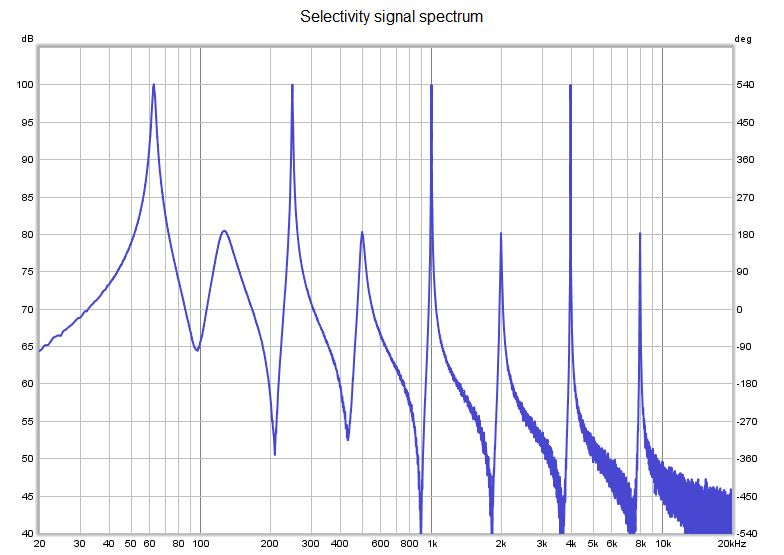
| + | <div style="text-align:justify;">Per aiutare a testare la selettività degli approcci classici e nel dominio della frequenza, è stato generato un segnale di test sintetico costituito da coseni di uguale ampiezza che decadono esponenzialmente alle frequenze centrali di un'ottava, con rumore aggiunto a -60 dB rispetto alle ampiezze del coseno. I tassi di decadimento del coseno di 60 dB si alternano tra 1.000 s e 0,100 s. Ecco lo spettro del segnale di prova.</div> | ||
| + | |||
| + | |||
| + | [[File:Selectivityspectrum.jpg]] | ||
| + | |||
| + | |||
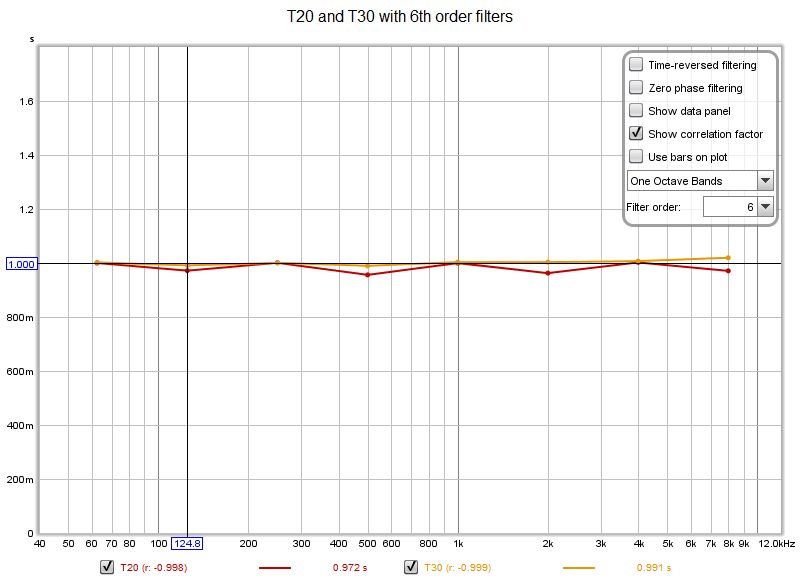
| + | Il segnale verrà filtrato in banda d'ottava in entrambi gli approcci. Considereremo innanzitutto l'approccio classico, partendo dai filtri del 6° ordine tipicamente utilizzati. | ||
| + | |||
| + | |||
| + | [[File:Selectivityorder6.jpg]] | ||
| + | |||
| + | |||
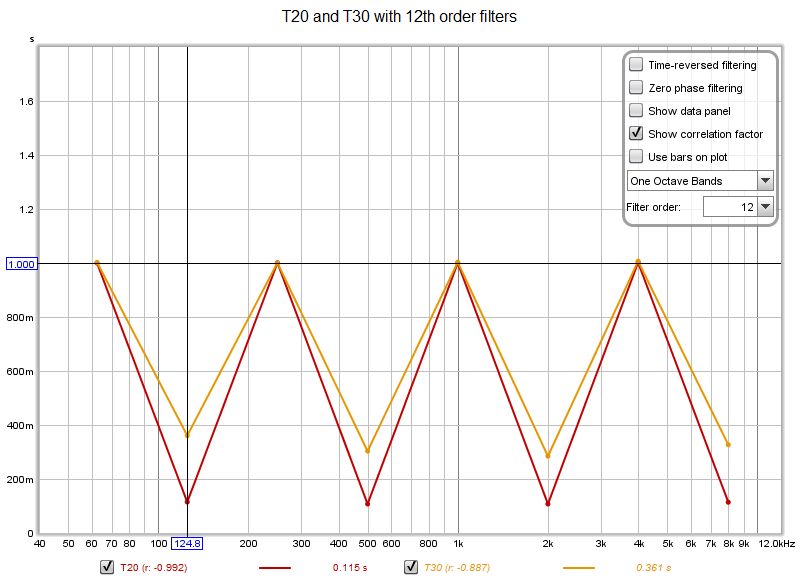
| + | Con i filtri del 6° ordine i decadimenti di 0,100 s non vengono affatto risolti. Proveremo successivamente i filtri del 12° ordine. | ||
| + | |||
| + | |||
| + | [[File:Selectivityorder12.jpg]] | ||
| + | |||
| + | |||
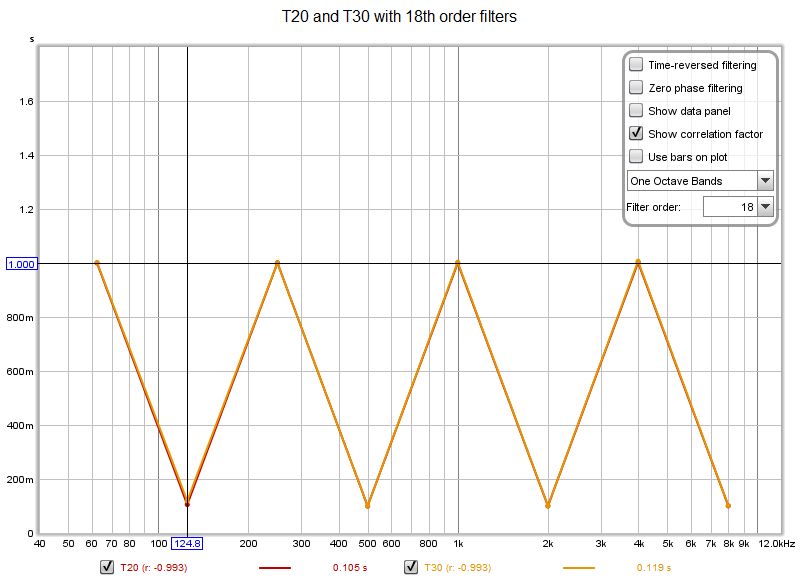
| + | I filtri del 12° ordine stanno iniziando a risolvere i decadimenti di 0,100 s, ma i risultati sono ancora lontani. Il prossimo sarà un filtro del 18° ordine. | ||
| + | |||
| + | |||
| + | [[File:Selectivityorder18.jpg]] | ||
| + | |||
| + | |||
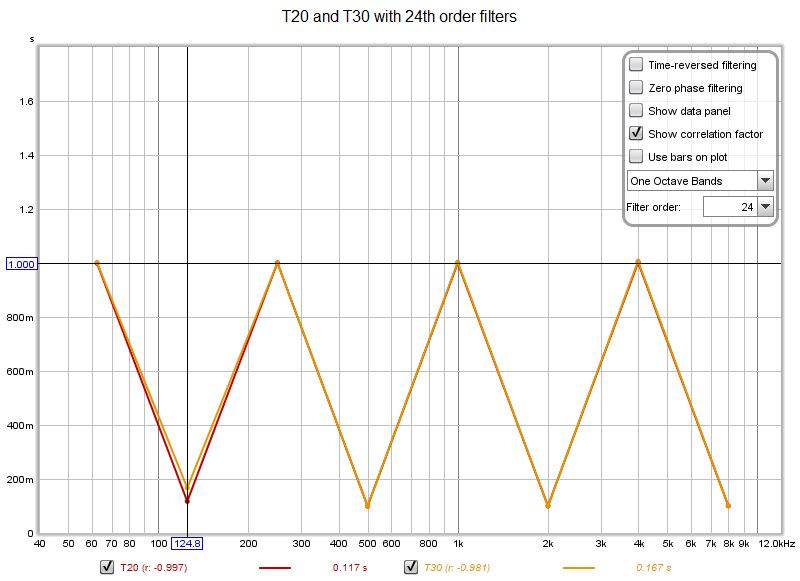
| + | <div style="text-align:justify;">I filtri del 18° ordine hanno risolto il problema, ad eccezione del decadimento più basso di 125 Hz 0,100 s, con T30 ancora leggermente peggiore di T20 in quel punto lì. L'aumento dell'ordine dei filtri peggiora ulteriormente i risultati anziché migliorarli, poiché i ritardi introdotti dal gruppo di filtri, iniziano a influenzare i risultati.</div> | ||
| + | |||
| + | |||
| + | [[File:Selectivityorder24.jpg]] | ||
| + | |||
| + | |||
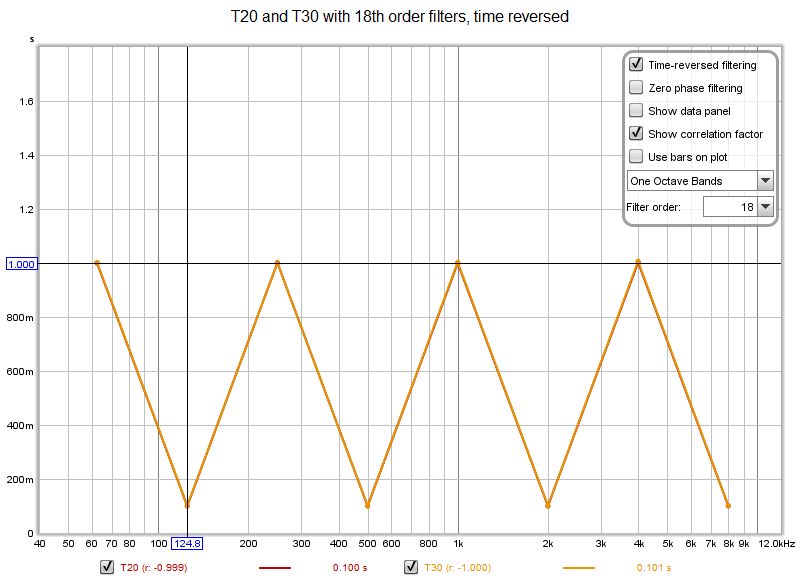
| + | Risultati perfetti possono essere ottenuti con filtri del 18° ordine e con filtri con inversione temporale. | ||
| + | |||
| + | |||
| + | [[File:Selectivityorder18timereversed.jpg]] | ||
| + | |||
| + | |||
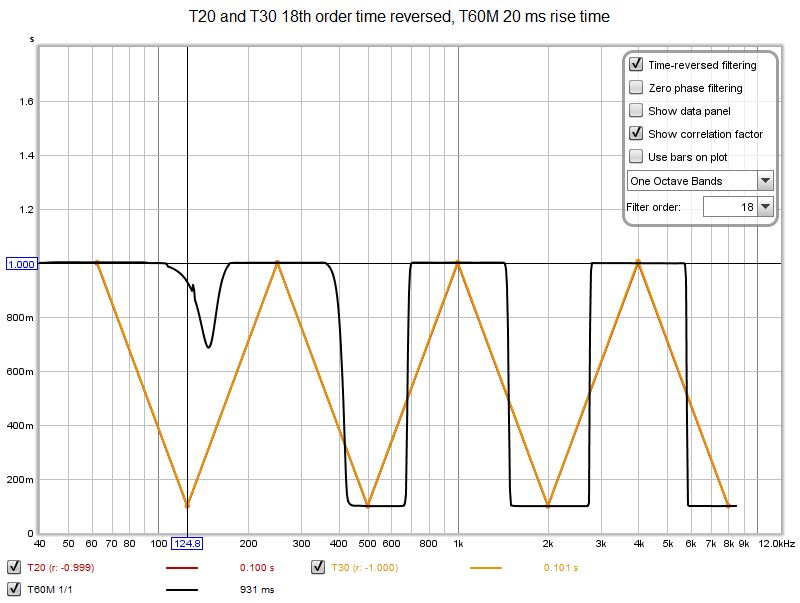
| + | <div style="text-align:justify;">Il risultato nel dominio della frequenza, dipende dalle impostazioni della finestra utilizzate. Per impostazione predefinita, REW sceglie un tempo di salita di 20 ms per questo segnale, fornendo i seguenti risultati (calcolati a 96 PPO anziché solo ai centri dell'ottava).</div> | ||
| + | |||
| + | |||
| + | [[File:Selectivityt60m20.jpg]] | ||
| + | |||
| + | |||
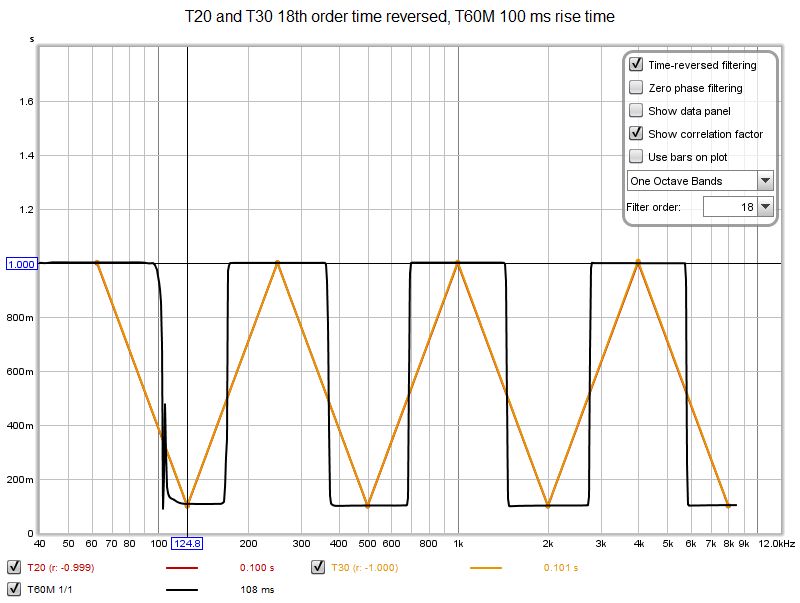
| + | Un tempo di salita di 100 ms migliora le prestazioni del T60M, anche se non riesce ancora ad eguagliare l'approccio classico con filtri a tempo invertito del 18° ordine al centro dell'ottava di 125 Hz. | ||
| + | |||
| + | |||
| + | [[File:Selectivityt60m100.jpg]] | ||
| + | |||
| + | |||
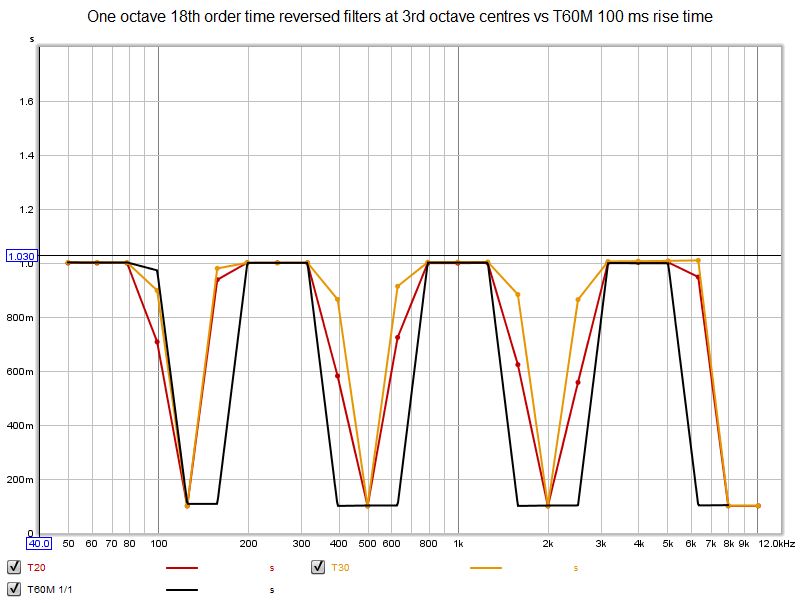
| + | <div style="text-align:justify;">Ulteriori aumenti del tempo di salita del T60M, migliorano la selettività ma degradano l'accuratezza del calcolo dell'RT60 a causa dell'effetto che l'utilizzo di finestre più ampie del tempo di decadimento, ha sui dati del decadimento stesso. Ciononostante si tratta di una buona prestazione dell'approccio alternativo, in particolare se confrontiamo il comportamento di entrambi gli approcci, lontano dai centri di un'ottava. Il grafico seguente utilizza un filtro con larghezza di banda di 1 ottava, tempo del 18° ordine invertito per T20 e T30, ma valuta anche il risultato alle frequenze centrali intermedie di un terzo di ottava. La T60M ha prestazioni decisamente migliori.</div> | ||
| + | |||
| + | |||
| + | [[File:Selectivityt60m100third.jpg]] | ||
| + | ---- | ||
| + | |||
| + | |||
| + | ===<span style="color:#4076c0;">'''''Confronto di precisione'''''</span>=== | ||
| + | |||
| + | |||
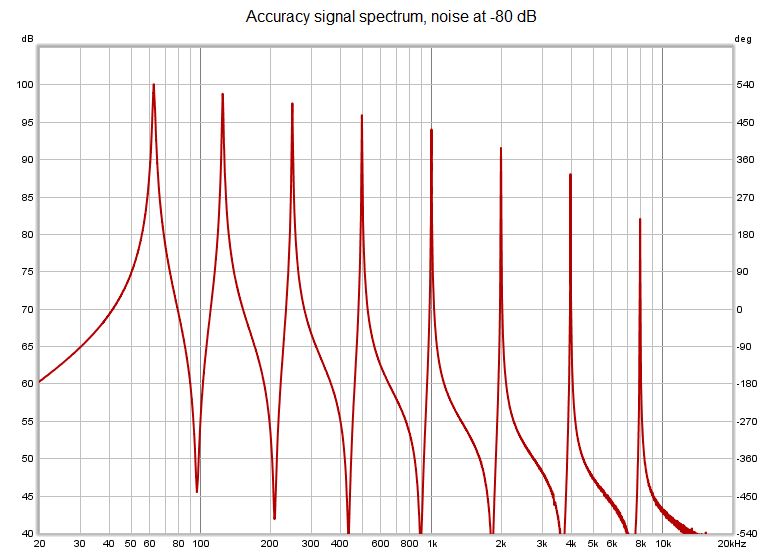
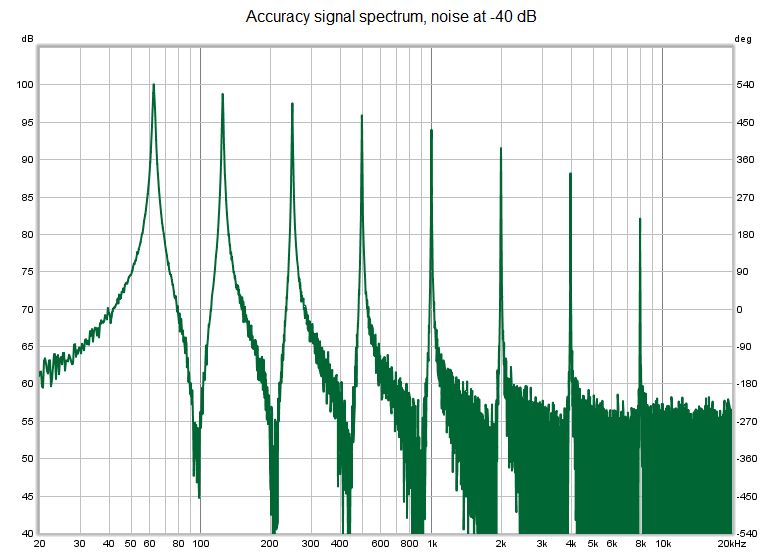
| + | <div style="text-align:justify;">Il prossimo test, riguarda la precisione. È stato generato un altro segnale di prova sintetico, anch'esso costituito da coseni con decadimento esponenziale di uguale ampiezza alle frequenze centrali di un'ottava, ma con tempi di decadimento di 60 dB che variavano in passi di 0,2 s da 1,600 s a 63 Hz a 0,200 s a 8 kHz. Il rumore è stato aggiunto a due diversi livelli, -80 dB per fungere da riferimento del segnale pulito e -40 dB per testare le prestazioni in presenza di rumore, in entrambi i casi rispetto alle ampiezze del coseno. Ecco gli spettri dei segnali di test.</div> | ||
| + | |||
| + | |||
| + | [[File:Accuracy80.jpg]] | ||
| + | |||
| + | |||
| + | [[File:Accuracy40.jpg]] | ||
| + | |||
| + | |||
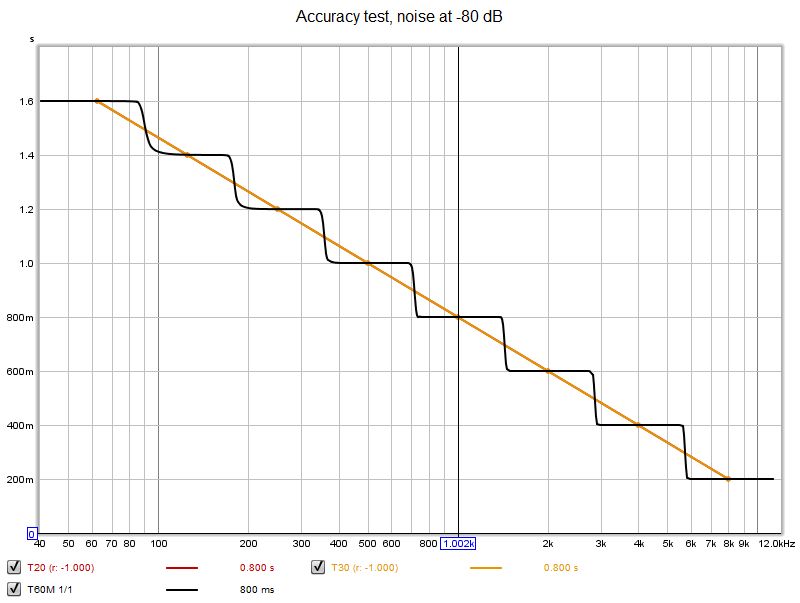
| + | Il segnale con rumore a -80 dB non ha presentato difficoltà né per gli approcci nuovi né per quelli classici. | ||
| + | |||
| + | |||
| + | [[File:Accuracy80rt60.jpg]] | ||
| + | |||
| + | |||
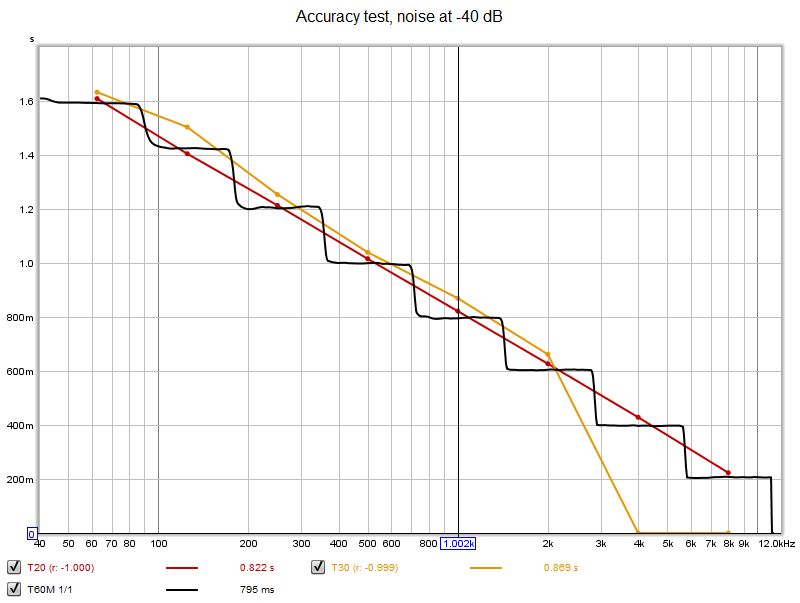
| + | <div style="text-align:justify;">Il segnale con rumore a -40 dB è stato più impegnativo per l'approccio classico, nonostante il rilevamento riuscito in tutti i casi, del rumore di fondo (utilizzando il metodo di Lundeby). L'ordine dei filtri ha apportato una differenza trascurabile e il 18° ordine ha fornito un miglioramento molto leggero. I risultati seguenti si riferiscono ai filtri del 18° ordine. Con questo segnale, l'approccio nel dominio della frequenza T60M, ha funzionato significativamente meglio dell'approccio classico.</div> | ||
| + | |||
| + | |||
| + | [[File:Accuracy40rt60.jpg]] | ||
| + | |||
| + | |||
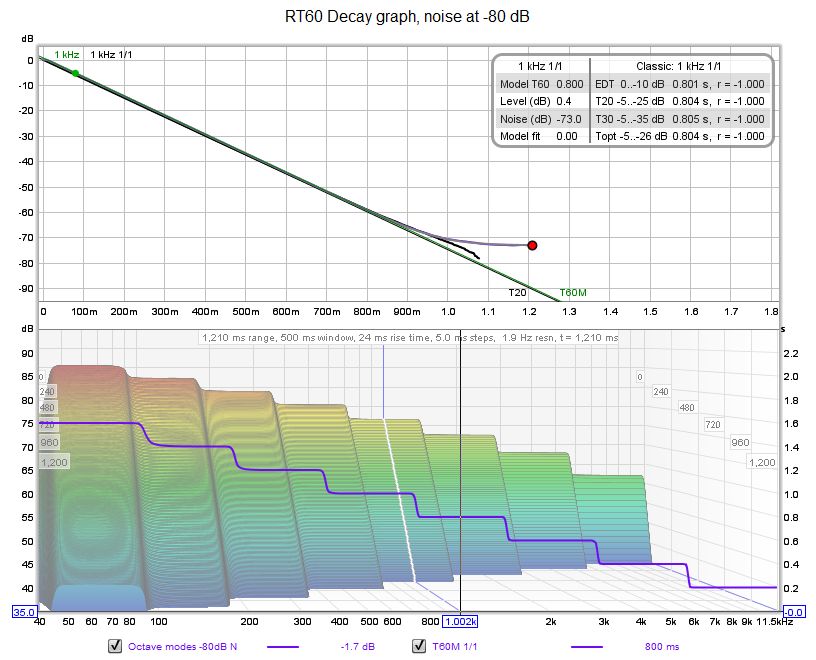
| + | Ecco alcuni esempi dei grafici di decadimento dell'RT60 per entrambi i casi. | ||
| + | |||
| + | |||
| + | [[File:Accuracy80decay.jpg]] | ||
| + | |||
| + | |||
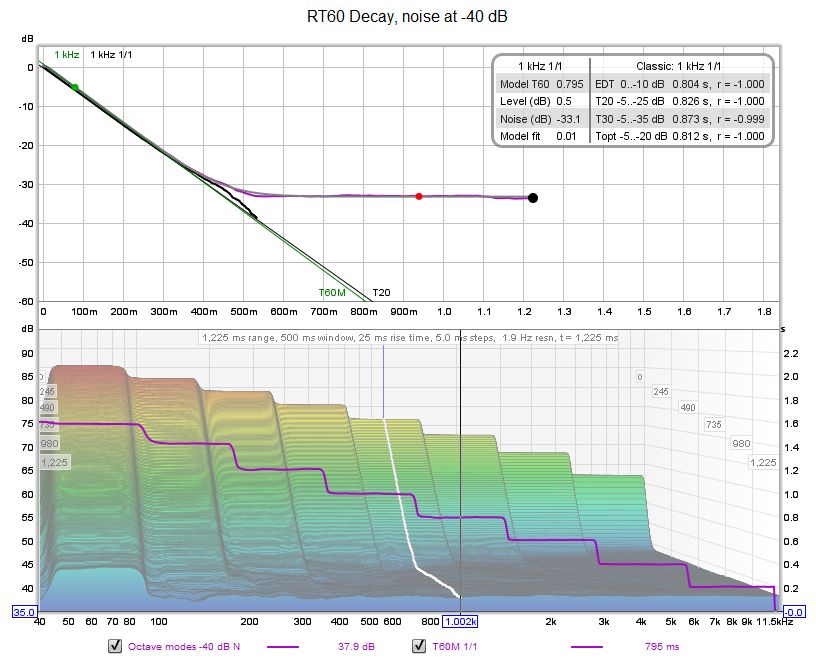
| + | [[File:Accuracy40decay.jpg]] | ||
| + | ---- | ||
| + | |||
| + | |||
| + | ===<span style="color:#4076c0;">'''''Implementazione'''''</span>=== | ||
| + | |||
| + | |||
| + | Ecco alcuni dettagli tecnici riguardanti l'implementazione in REW dell'analisi del decadimento dell'RT60. | ||
| + | |||
| + | |||
| + | ===<span style="color:#4076c0;">'''Dati di decadimento'''</span>=== | ||
| + | |||
| + | <div style="text-align:justify;">I dati di decadimento derivano da una serie di trasformate di Fourier, denominate fette. La prima fetta, utilizza come punto di riferimento il picco della risposta all'impulso e ogni fetta successiva viene spostata nel tempo dell'intervallo della fetta stessa. L'intervallo di tempo totale coperto dalle sezioni è specificato nell'impostazione "Range". Ciascuna fetta è finestrata con una finestra di Hann sul lato sinistro la cui larghezza è pari al tempo di salita e una finestra di Hann sul lato destro uguale alla larghezza della "finestra". Da notare che alle alte frequenze il rumore di fondo in un approccio nel dominio della frequenza sarà tipicamente più elevato rispetto ad un approccio classico, a causa dell'ampiezza della finestra FFT richiesta per la gamma delle basse frequenze. Finestre più strette e tempi di salita più brevi, potrebbero essere utilizzati per generare dei dati di decadimento delle alte frequenze con livelli di rumore inferiori. Si potrebbe prendere in considerazione un approccio con finestre dipendenti dalla frequenza (FDW), ma le implementazioni FDW in genere hanno finestre simmetriche che comporterebbero un tempo di salita eccessivo alle basse frequenze.</div><br> | ||
| + | <div style="text-align:justify;">Le impostazioni '''Automatic''', ricavano l'intervallo di tempo eseguendo un'analisi T20 convenzionale utilizzando filtri di 6° ordine da 1 ottava a 250, 500 e 1000 Hz. Come intervallo di tempo viene utilizzato il valore T20 più lungo, con un valore minimo di 500 ms. L'intervallo di slice è impostato per fornire circa 250 slice nell'intervallo, con un passo di slice massimo di 100 ms. Il tempo di salita è impostato al 2% dell'intervallo, con un massimo di 400 ms.</div><br> | ||
| + | <div style="text-align:justify;">I dati per ciascuna fetta vengono filtrati con un filtro passa-basso a 1/48 di ottava, quindi campionati a 96 punti per ottava per fornire un set di dati distanziati logaritmicamente. Il successivo filtraggio in banda di ottava, viene applicato alle grandezze al quadrato di quei dati distanziati logaritmicamente, utilizzando un kernel che è unitario su tutta la larghezza della banda tranne che alle estremità, dove la sua ampiezza è pari a 0,5.</div> | ||
| + | |||
| + | |||
| + | ===<span style="color:#4076c0;">'''Analisi RT60'''</span>=== | ||
| + | |||
| + | <div style="text-align:justify;">Per il calcolo RT60, viene analizzata la serie di dati formata dai valori di ciascuna fetta ad una certa frequenza. Di questi dati, viene eseguita una scansione iniziale per determinare se ci sono bruschi rallentamenti o aumenti verso la fine e se vengono trovati dati successivi, questi vengono esclusi dall'analisi.</div> | ||
| + | L'analisi consiste nell'adattare ai dati una funzione esponenziale di decadimento più rumore. La funzione è: | ||
| + | |||
| + | f(t) = level*exp(-6*log(10)*t/t60) + noise | ||
| + | |||
| + | <div style="text-align:justify;">I tre parametri del modello, livello, t60 e rumore, sono determinati minimizzando una funzione di errore formata dalla differenza tra il valore della funzione e i dati di decadimento ai tempi di slice. REW utilizzerà il valore quadratico medio della differenza tra i dati di decadimento in dB e i valori in dB della funzione del modello, ponderato da una funzione di ridimensionamento dell'errore che attribuisce meno peso ai valori inferiori a -20 dB. Le stime iniziali per i parametri del modello si basano su una linea dei minimi quadrati adattata ai dati di decadimento nell'intervallo da -10 a -20 dB.</div><br> | ||
| + | <div style="text-align:justify;">L'errore del modello viene valutato su una sottosezione dei dati di decadimento. Il punto di inizio nominale per l'adattamento del modello è il punto a -5 dB sulla curva di decadimento, ma collocato dopo il suo inizio di almeno 10 ms o quanto il tempo di salita e con un limite generale che non sia superiore a 10 dB lungo la curva dello stesso. Va tenuto presente che, a differenza di un integrale di Schroeder, i dati di decadimento tipicamente non sono monotoni, quindi il "punto a -5 dB" si riferisce all'ultimo punto della risposta dove essa passa attraverso i -5 dB. L'adattamento di REW del metodo di Lundeby, viene applicato ai dati di magnitudo quadrata del decadimento, per stimare il rumore di fondo e l'intersezione del rumore di fondo con la linea di decadimento RT60. L'indice finale di adattamento viene quindi impostato due volte più lontano nella curva di decadimento rispetto a quel punto di intersezione. Se la routine di Lundeby non trova un buon risultato, la fine adattata corrisponde alla fine dei dati validi.</div><br> | ||
| + | <div style="text-align:justify;">Per trovare i parametri ottimali del modello, viene utilizzato un port Java di UNCMIN (di Steve Verrill). UNCMIN è un ottimizzatore non vincolato, i cui vincoli vengono impostati modificando le voci del vettore di minimizzazione prima che vengano utilizzate nella funzione del modello. Questo processo di vincolo fa parte di una trasformazione dei valori dei parametri dallo spazio dell'ottimizzatore fino allo spazio delle funzioni. I parametri nello spazio del minimizzatore corrispondenti al livello e al rumore, sono equivalenti in dB scalati dei valori del modello. Il parametro di minimizzazione corrispondente a t60 è un reciproco scalato del valore T60. I limiti ai valori vengono posti in base alle stime iniziali.</div><br> | ||
| + | <div style="text-align:justify;">Una buona selettività alle basse frequenze, richiede tempi di salita tipicamente maggiori dell'intervallo di fetta. L'effetto della finestra di sinistra sui dati di decadimento deve essere preso in considerazione prima di valutare l'errore di adattamento del modello. La finestra di sinistra è coinvolta con i dati di decadimento, ma non con i valori di decadimento di ogni singola fetta ma piuttosto con le differenze tra i valori di decadimento per le fette successive, poiché è su questa differenza che la finestra agisce.</div> | ||
| + | ---- | ||
[[Indice dei contenuti]] - [[#top|Torna su]] | [[Indice dei contenuti]] - [[#top|Torna su]] | ||
Versione attuale delle 07:42, 18 ott 2023
Indice
Grafico del decadimento dell'RT60
Stima dell'RT60 nel dominio della frequenza
Stima classica dell'RT60
Un approccio nel dominio della frequenza alla stima dell'RT60
L'integrale di Schroeder non è applicabile all'elaborazione effettuata nel dominio della frequenza. Le porzioni STFT catturano i decadimenti del riverbero e il rumore e i tempi di riverbero possono essere stimati adattando una funzione esponenziale del decadimento più il rumore, alla serie di dati formata dai valori delle porzioni in ogni intervallo di tempo. Il processo di adattamento deve tenere conto dell'effetto della finestra di sinistra sulla serie di dati, dove la sua larghezza è maggiore dell'intervallo delle sezioni. Inoltre, deve anche essere tollerante nei confronti della natura non monotona dei dati di decadimento.
Il pannello di controllo nel grafico inferiore è dotato di un pulsante per calcolare il modello dell'RT60.
Dopo che è stato effettuato il calcolo del modello, il risultato può essere visualizzato anche sul grafico RT60, consentendone un facile confronto con le misure classiche.
Confronto di selettività
Il segnale verrà filtrato in banda d'ottava in entrambi gli approcci. Considereremo innanzitutto l'approccio classico, partendo dai filtri del 6° ordine tipicamente utilizzati.
Con i filtri del 6° ordine i decadimenti di 0,100 s non vengono affatto risolti. Proveremo successivamente i filtri del 12° ordine.
I filtri del 12° ordine stanno iniziando a risolvere i decadimenti di 0,100 s, ma i risultati sono ancora lontani. Il prossimo sarà un filtro del 18° ordine.
Risultati perfetti possono essere ottenuti con filtri del 18° ordine e con filtri con inversione temporale.
Un tempo di salita di 100 ms migliora le prestazioni del T60M, anche se non riesce ancora ad eguagliare l'approccio classico con filtri a tempo invertito del 18° ordine al centro dell'ottava di 125 Hz.
Confronto di precisione
Il segnale con rumore a -80 dB non ha presentato difficoltà né per gli approcci nuovi né per quelli classici.
Ecco alcuni esempi dei grafici di decadimento dell'RT60 per entrambi i casi.
Implementazione
Ecco alcuni dettagli tecnici riguardanti l'implementazione in REW dell'analisi del decadimento dell'RT60.
Dati di decadimento
Analisi RT60
L'analisi consiste nell'adattare ai dati una funzione esponenziale di decadimento più rumore. La funzione è:
f(t) = level*exp(-6*log(10)*t/t60) + noise