Segnali e misure: differenze tra le versioni
(→Segnali, Frequenza di campionamento e Risoluzione) |
(→Segnali e Misure) |
||
| Riga 12: | Riga 12: | ||
<div align="justify">La risoluzione delle misure della scheda audio, è tipicamente pari a 16 bit o 24 bit. La risoluzione a 16 bit, è la stessa utilizzata nei CD ed è supportata da REW. Avere 16 bit di risoluzione, significa che il range dei valori di una misura, è compreso tra -32768 e +32767 (numeri che possono essere rappresentati con 15 cifre binarie, più la 16^ cifra che indica il segno del numero). Anziché utilizzare direttamente i numeri della misura, è conveniente fare riferimento ad essi in termini di quanto si avvicinano al numero più grande e ciò rappresenta il Full Scale ed è abbreviato come FS. I valori full scale sono -32768 e +32767. Il più piccolo valore di misura diverso da zero, è 1, che come percentuale del full scale è 100 x (1/32768) o, approssimativamente lo 0.003% FS. Tutto ciò che è più piccolo di questo valore, è visto dalla scheda audio come zero. Il valore full scale, corrisponderà ad una certa tensione agli ingressi della scheda audio, che normalmente si aggira intorno a 1 Volt. Le schede audio che hanno una risoluzione maggiore (24 bit), generalmente hanno lo stessa tensione massima di ingresso (circa 1 Volt) ma possono usare una gamma maggiore di numeri per misurare la tensione di ingresso. Per una scheda audio a 24-bit, il numero di valori full scale varia da -8388608 a +8388607. Questo rappresenta ancora solo 1 Volt (tipicamente). Il valore più grande non è cambiato ma è cambiata la risoluzione che, per una scheda audio a 24-bit, equivale a misurare il più piccolo valore pari a 100 x (1/8388608) percentuale del full scale, cioè 0.000012% FS. Quindi, la maggior risoluzione offre benefici nella misura di segnali molto piccoli. Il valore full scale è spesso trattato come corrispondente al valore uno e tutto ciò che si trova sotto tale valore rispetto al full scale, è considerato come la corrispondente proporzione di uno. Così mezzo full scale sarà 0.5 e così via.</div> | <div align="justify">La risoluzione delle misure della scheda audio, è tipicamente pari a 16 bit o 24 bit. La risoluzione a 16 bit, è la stessa utilizzata nei CD ed è supportata da REW. Avere 16 bit di risoluzione, significa che il range dei valori di una misura, è compreso tra -32768 e +32767 (numeri che possono essere rappresentati con 15 cifre binarie, più la 16^ cifra che indica il segno del numero). Anziché utilizzare direttamente i numeri della misura, è conveniente fare riferimento ad essi in termini di quanto si avvicinano al numero più grande e ciò rappresenta il Full Scale ed è abbreviato come FS. I valori full scale sono -32768 e +32767. Il più piccolo valore di misura diverso da zero, è 1, che come percentuale del full scale è 100 x (1/32768) o, approssimativamente lo 0.003% FS. Tutto ciò che è più piccolo di questo valore, è visto dalla scheda audio come zero. Il valore full scale, corrisponderà ad una certa tensione agli ingressi della scheda audio, che normalmente si aggira intorno a 1 Volt. Le schede audio che hanno una risoluzione maggiore (24 bit), generalmente hanno lo stessa tensione massima di ingresso (circa 1 Volt) ma possono usare una gamma maggiore di numeri per misurare la tensione di ingresso. Per una scheda audio a 24-bit, il numero di valori full scale varia da -8388608 a +8388607. Questo rappresenta ancora solo 1 Volt (tipicamente). Il valore più grande non è cambiato ma è cambiata la risoluzione che, per una scheda audio a 24-bit, equivale a misurare il più piccolo valore pari a 100 x (1/8388608) percentuale del full scale, cioè 0.000012% FS. Quindi, la maggior risoluzione offre benefici nella misura di segnali molto piccoli. Il valore full scale è spesso trattato come corrispondente al valore uno e tutto ciò che si trova sotto tale valore rispetto al full scale, è considerato come la corrispondente proporzione di uno. Così mezzo full scale sarà 0.5 e così via.</div> | ||
| + | |||
| + | |||
| + | ===Clipping=== | ||
| + | |||
| + | Se il segnale è maggiore del valore full scale che la scheda audio è in grado di trattare, il valore della misura non potrà essere in ogni caso maggiore del valore full scale, qualsiasi cosa succeda all’ingresso. Quando il segnale è andato al di là del range che l’ingresso è in grado di misurare, si dice che che questo è clippato. Il clipping è visualizzato come una parte piatta della risposta. Se avviene all’ingresso della scheda audio, sarà a +100% FS o a -100% FS e REW vi avviserà, ma talvolta, il clipping avviene prima che il segnale raggiunga | ||
| + | |||
| + | la scheda audio (per esempio, nel preamplificatore microfonico, se è stato impostato un guadagno troppo elevato). In questo caso, la misura del valore, non arriverà mai al valore FS della scheda audio, ma il segnale sarà comunque clippato. Il clipping deve essere evitato durante la misura, perchè il segnale catturato, non rappresenta più ciò che realmente accade all’ingresso e che ha corrotto la misura. | ||
| Riga 24: | Riga 31: | ||
<div align="justify">Quando, per calcolare lo spettro, facciamo uso della FFT, essa usa un pacchetto di frequenze che, uniformemente distanziate, partono dalla DC (frequenza zero) fino alla metà della frequenza di campionamento (il massimo che può essere correttamente rappresentato). La spaziatura, dipende dalla lunghezza del segnale che intendiamo analizzare con la FFT. I calcoli della FFT, sono molto più efficienti, quando le lunghezze dei segnali, sono potenze di 2, come 16k (16,384), 32k (32768) o 64k (65536). Per calcolare la FFT a 64k di un segnale che è campionato a 48kHz, abbiamo bisogno di 65536/48000 secondi di segnale, cioè 1.365s. Le frequenze, saranno spaziate di 24000/65536 = 0.366Hz. Se la FFT è stata generata da campioni a 16k, le frequenze sarebbero spaziate di 1.465Hz. Più le frequenze sono tra loro distanti, minore è la risoluzione in frequenza. Per una alta risoluzione in frequenza, dobbiamo analizzare i segnali per un lungo periodo di tempo.</div> | <div align="justify">Quando, per calcolare lo spettro, facciamo uso della FFT, essa usa un pacchetto di frequenze che, uniformemente distanziate, partono dalla DC (frequenza zero) fino alla metà della frequenza di campionamento (il massimo che può essere correttamente rappresentato). La spaziatura, dipende dalla lunghezza del segnale che intendiamo analizzare con la FFT. I calcoli della FFT, sono molto più efficienti, quando le lunghezze dei segnali, sono potenze di 2, come 16k (16,384), 32k (32768) o 64k (65536). Per calcolare la FFT a 64k di un segnale che è campionato a 48kHz, abbiamo bisogno di 65536/48000 secondi di segnale, cioè 1.365s. Le frequenze, saranno spaziate di 24000/65536 = 0.366Hz. Se la FFT è stata generata da campioni a 16k, le frequenze sarebbero spaziate di 1.465Hz. Più le frequenze sono tra loro distanti, minore è la risoluzione in frequenza. Per una alta risoluzione in frequenza, dobbiamo analizzare i segnali per un lungo periodo di tempo.</div> | ||
| − | |||
| − | <div align="justify"> | + | ===RTA=== |
| + | <div align="justify">Un modo comune per visualizzare lo spettro di un segnale di tempo, è l'utilizzo di un Real Time Analyser o RTA. L' RTA mostra un grafico delle ampiezze delle frequenze dei segnali che sta analizzando. Tuttavia, mentre la FFT produce segnali che sono a frequenze uniformemente distanziate, un RTA le raggruppa insieme in frazioni di ottava. Un'ottava, equivale ad un raddoppio della frequenza, così, l'intervallo tra 100Hz e 200Hz equivale ad un'ottava, così come l'intervallo tra 1kHz e 2kHz. L'intervallo di frequenza di una frazione di ottava, è maggiore della frequenza che si ottiene. Per una RTA a 1/3 di ottava, l'intervallo è di 4.6Hz a 20Hz, ma è di 4.6kHz a 20kHz. Per una RTA a 1/24 di ottava, gli intervalli sono 1/8 più larghi. All'interno dell'intervallo di una frazione di ottava, molti singoli valori FFT possono essere usati per produrre il singolo valore che l'RTA assegna a quella banda di frequenze. In basso, è visualizzata un'immagine dell'RTA di REW che mostra lo spettro di un tono a 1KHz e la sua distorsione armonica.</div> | ||
Versione delle 17:44, 15 apr 2016
Indice
[nascondi]Segnali e Misure
"Cosa significa tutta questa roba?"
Segnali, Frequenza di campionamento e Risoluzione
Clipping
Se il segnale è maggiore del valore full scale che la scheda audio è in grado di trattare, il valore della misura non potrà essere in ogni caso maggiore del valore full scale, qualsiasi cosa succeda all’ingresso. Quando il segnale è andato al di là del range che l’ingresso è in grado di misurare, si dice che che questo è clippato. Il clipping è visualizzato come una parte piatta della risposta. Se avviene all’ingresso della scheda audio, sarà a +100% FS o a -100% FS e REW vi avviserà, ma talvolta, il clipping avviene prima che il segnale raggiunga
la scheda audio (per esempio, nel preamplificatore microfonico, se è stato impostato un guadagno troppo elevato). In questo caso, la misura del valore, non arriverà mai al valore FS della scheda audio, ma il segnale sarà comunque clippato. Il clipping deve essere evitato durante la misura, perchè il segnale catturato, non rappresenta più ciò che realmente accade all’ingresso e che ha corrotto la misura.
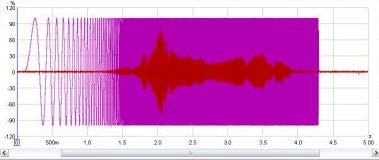
Visualizzare i segnali