Fase minima: differenze tra le versioni
Da REW Wiki.
| Riga 31: | Riga 31: | ||
[[File:group_delay.png]] | [[File:group_delay.png]] | ||
| + | |||
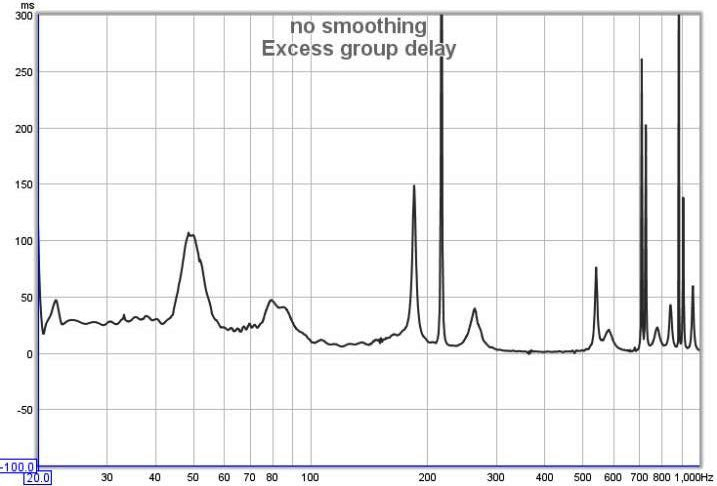
| + | <div align="justify">Guardando un pò più da vicino, possiamo ipotizzare che, i luoghi nel ritardo di gruppo, dove ci sono oscillazioni particolarmente rilevanti, non sono a fase minima, ma questo non ci permette ancora di identificare facilmente le regioni a fase minima. Per fare questo, dobbiamo comparare la misura, con un sistema che ha stessa risposta in ampiezza ma è a fase minima e guardare alla misura del ritardo di gruppo in eccesso. La risposta a fase minima, è generata utilizzando l’ampiezza della misura, e calcolando da essa, la corrispondente fase minima, utilizzando una relazione matematica tra le due che vale per i sistemi a fase minima. Osservando la differenza tra quanto misurato e la fase minima (la fase in eccesso) e misurando la pendenza di tale differenza per trovare il ritardo di gruppo in eccesso, otterremo questo grafico:</div> | ||
| + | |||
| + | [[File:exc_group_delay.png]] | ||
Versione delle 09:06, 19 mag 2016
Indice
Fase minima
Nelle discussioni relative all’equalizzazione ed in particolare a quella applicata al tentativo di migliorare la risposta acustica di una stanza, spesso affiora il termine “fase minima”, che generalmente rientra in un contesto che definisce se l’equalizzazione può o non può essere usata con successo per risolvere un problema di risposta. Quindi, che cos’è la “fase minima” e perchè dovremmo preoccuparcene?
Esistono formule matematiche rigorose e definizioni della teoria dei sistemi che definiscono cosa costituisce un sistema a fase minima, ma non lo ripeterò in questa sede. Nel contesto delle misure acustiche, un sistema a fase minima, possiede due importanti proprietà: introduce il più basso ritardo ai segnali che lo attraversano e può essere invertito.
Esistono formule matematiche rigorose e definizioni della teoria dei sistemi che definiscono cosa costituisce un sistema a fase minima, ma non lo ripeterò in questa sede. Nel contesto delle misure acustiche, un sistema a fase minima, possiede due importanti proprietà: introduce il più basso ritardo ai segnali che lo attraversano e può essere invertito.
Fase minima e Tempo di ritardo
La proprietà "lowest time delay" (più basso tempo di ritardo), si riferisce alla quantità delle componenti ritardate in frequenza di un segnale, che allo stesso tempo forniscono la risposta in frequenza misurata (SPL). Possiamo vedere le caratteristiche di ritardo, direttamente nel grafico Group Delay del sistema. Data una risposta in frequenza misurata, non siamo in grado di stabilire dalla sola risposta SPL, se ciò che abbiamo rilevato, possiede la caratteristica di “minimo ritardo”. Se da qualche parte nel sistema, esiste un ritardo come quello impiegato dal suono per viaggiare dall’altoparlante al microfono, quel ritardo rappresenta la fase non-minima (nel senso stretto del termine) ma non altera la risposta SPL che abbiamo misurato.
Un ritardo, causa uno sfasamento che aumenta con la frequenza. Per esempio, un ritardo di appena 1ms, produce uno sfasamento di 36 gradi a 100Hz, ma lo sfasamento diventa di 3600 gradi a 10kHz, poichè 1ms è 1/10 del periodo di 10ms di un segnale a 100Hz ma è 10 volte il periodo di 0,1ms di un segnale a 10kHz, e ogni periodo è di 360 gradi.
Lo sfasamento causato dal ritardo, è lineare con la frequenza. Ciò significa per esempio, che 1ms di ritardo produrrà uno sfasamento di 36 gradi a 100Hz, 2 ms a 200Hz, 3ms a 300Hz e così via. Se l’asse della frequenza è stato impostato su lineare, il grafico della fase di un ritardo, si presenterà come una linea retta che decresce all’aumentare della frequenza. Quanto ripidamente questa decresce, è determinato da quanto grande è il ritardo.
Mentre i ritardi costanti rendono difficile interpretare la risposta di fase, la loro rimozione dalle nostre misure, non causerà nessun problema con l’applicazione dell’EQ. Tuttavia, la loro rimozione (o il loro effetto), non è sufficiente a rendere un sistema a fase minima ma c'è dell'altro da fare.
Fase minima e Invertibilità
I sistemi a fase minima, possono essere invertiti, che significa che un filtro, può essere progettato in modo che, se applicato al sistema, produca una risposta piatta e corregga la risposta di fase allo stesso tempo. Questa è chiaramente una proprietà interessante da ricercare se vogliamo applicare l’EQ. Se applichiamo l’EQ ad un sistema che non è a fase minima, o più in particolare in una regione dove non è a fase minima, l’EQ non produrrà i risultati sperati. Potrebbe essere ancora possibile ottenere una risposta piatta, ma correggendo la risposta di fase, tale operazione non è possibile.
Un semplice esempio di qualcosa che renda l’idea di una risposta a fase non-minima, sono le riflessioni che sono grandi o più grandi del segnale diretto (le riflessioni lungo percorsi che sono differenti ma con la stessa lunghezza, possono combinarsi per produrre livelli più alti, o le superfici curve, possono focalizzare una riflessione). Nel caso semplice di una riflessione che ha esattamente la stessa ampiezza del segnale diretto, troveremo delle frequenze regolarmente distanziate alle quali la riflessione è sfasata di 180° rispetto al suono diretto. Quando questi segnali si combinano, il risultato è ampiezza zero a quelle frequenze (un esempio estremo del filtraggio a pettine spesso incontrato nelle misure acustiche). Tale livello zero, non può essere ripristinato al suo valore iniziale, da nessuna quantità di equalizzazione, poichè agendo questa equamente sia sul segnale diretto che su quello riflesso, il segnale continuerebbe ad essere cancellato. Se la risposta contiene regioni che sono a zero, queste non possono essere invertite e non sono a fase minima. Se le riflessioni sono più grandi del suono diretto, il problema è altrettanto importante come anche se non avessimo più un livello zero, ci troveremmo nella situazione finale dove le correzioni che l’EQ sta applicando, dovrebbero continuare ad essere più grandi, per contrastare la sempre più grande riflessione raggiungendo velocemente il limite massimo.
Identificare le regioni a fase minima
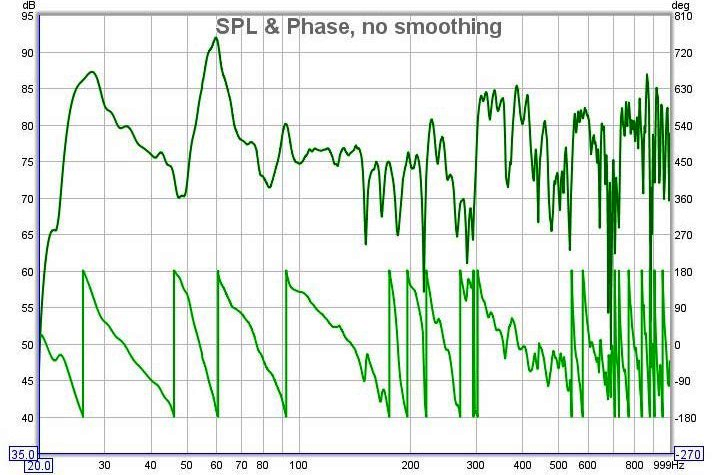
Le risposte di una stanza, sono a fase mista. Ciò significa che ci sono regioni a fase minima e regioni che non sono a fase minima. Le regioni a fase minima, tendono a manifestarsi a bassa frequenza ma non possiamo semplicemente dire che una risposta è a fase minima al di sotto di alcuni specifici tagli. Non è possibile identificare regioni a fase minima semplicemente guardando la risposta di fase complessiva, specialmente se la misura non mostra alcun ritardo. La risposta dettagliata, fornisce invece un maggior numero di dettagli, tracciati ungo l’asse lineare della frequenza, ma spesso copre un intervallo talmente grande, da risultare inutilizzabile. Anche se dovessimo rimuovere ogni ritardo nella misura, la sola risposta di fase non ci permetterebbe ancora di identificare facilmente le regioni a fase minima. Vi è tuttavia, un metodo semplice. Qui la misura di un sistema sub + altoparlanti principali in una stanza:
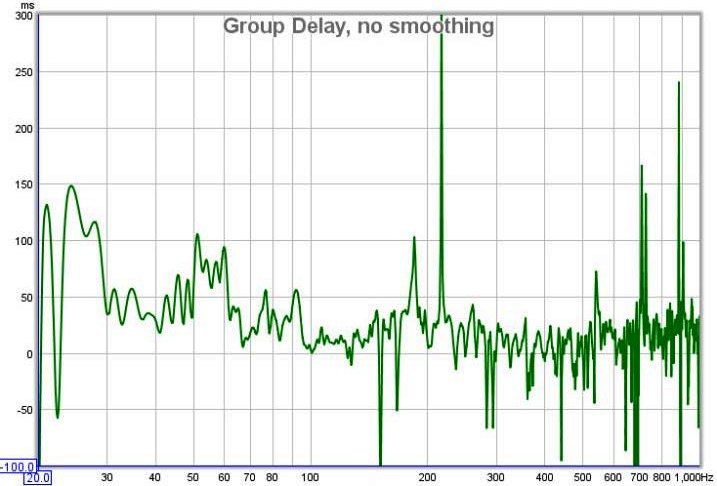
Possiamo tentare di indovinare che si tratta principalmente di fase minima al di sotto della frequenza di transizione della stanza e di fase non minima al di sopra, ma per evitare congetture, diamo un’occhiata al ritardo di gruppo. Il grafico del ritardo di gruppo ci mostra di quanto ciascuna frequenza è stata ritardata. Matematicamente è il grafico della pendenza della fase scompattata, così ovunque quella fase decresce linearmente, corrisponde ad una regione con ritardo di gruppo costante (quella regione è ritardata da una quantità di tempo costante). Nell’immagine il grafico del ritardo di gruppo relativo alla misura:
Guardando un pò più da vicino, possiamo ipotizzare che, i luoghi nel ritardo di gruppo, dove ci sono oscillazioni particolarmente rilevanti, non sono a fase minima, ma questo non ci permette ancora di identificare facilmente le regioni a fase minima. Per fare questo, dobbiamo comparare la misura, con un sistema che ha stessa risposta in ampiezza ma è a fase minima e guardare alla misura del ritardo di gruppo in eccesso. La risposta a fase minima, è generata utilizzando l’ampiezza della misura, e calcolando da essa, la corrispondente fase minima, utilizzando una relazione matematica tra le due che vale per i sistemi a fase minima. Osservando la differenza tra quanto misurato e la fase minima (la fase in eccesso) e misurando la pendenza di tale differenza per trovare il ritardo di gruppo in eccesso, otterremo questo grafico: