Grafico del decadimento dell'RT60: differenze tra le versioni
(→Stima classica dell'RT60) |
(→Un approccio nel dominio della frequenza alla stima dell'RT60) |
||
| Riga 29: | Riga 29: | ||
===<span style="color:#4076c0;">'''''Un approccio nel dominio della frequenza alla stima dell'RT60'''''</span>=== | ===<span style="color:#4076c0;">'''''Un approccio nel dominio della frequenza alla stima dell'RT60'''''</span>=== | ||
<div style="text-align:justify;">I tempi di riverbero possono anche essere stimati attraverso l'elaborazione effettuata nel dominio della frequenza, esaminando i decadimenti delle sezioni di un insieme di grafici della trasformata di Fourier a tempo breve (STFT). Questi sono comunemente usati per produrre grafici a cascata o spettrogrammi. Le fette di una serie STFT possono essere filtrate in banda d'ottava nel dominio della frequenza utilizzando filtri brick wall senza nessun ritardo di gruppo associato nel dominio del tempo. La discriminazione di frequenza è quindi determinata dalle caratteristiche della finestra utilizzata per l'STFT, il cui fattore decisivo generalmente è determinato dalla larghezza e dalla forma del lato sinistro della finestra (noto anche come tempo di salita della finestra). L'elaborazione nel dominio della frequenza rende perciò semplice la presentazione dei risultati utilizzando dei filtri a banda d'ottava molto più stretti, consentendo quindi di distinguere le singole risonanze senza alcun impatto negativo sulla stima del tempo di riverbero.<br> | <div style="text-align:justify;">I tempi di riverbero possono anche essere stimati attraverso l'elaborazione effettuata nel dominio della frequenza, esaminando i decadimenti delle sezioni di un insieme di grafici della trasformata di Fourier a tempo breve (STFT). Questi sono comunemente usati per produrre grafici a cascata o spettrogrammi. Le fette di una serie STFT possono essere filtrate in banda d'ottava nel dominio della frequenza utilizzando filtri brick wall senza nessun ritardo di gruppo associato nel dominio del tempo. La discriminazione di frequenza è quindi determinata dalle caratteristiche della finestra utilizzata per l'STFT, il cui fattore decisivo generalmente è determinato dalla larghezza e dalla forma del lato sinistro della finestra (noto anche come tempo di salita della finestra). L'elaborazione nel dominio della frequenza rende perciò semplice la presentazione dei risultati utilizzando dei filtri a banda d'ottava molto più stretti, consentendo quindi di distinguere le singole risonanze senza alcun impatto negativo sulla stima del tempo di riverbero.<br> | ||
| − | L'integrale di Schroeder non è applicabile all'elaborazione effettuata nel dominio della frequenza. Le porzioni STFT catturano i decadimenti del riverbero e il rumore e i tempi di riverbero possono essere stimati adattando una funzione esponenziale del decadimento più il rumore, alla serie di dati formata dai valori delle porzioni in ogni intervallo di tempo. Il processo di adattamento deve tenere conto dell'effetto della finestra di sinistra sulla serie di dati, dove la sua larghezza è maggiore dell'intervallo delle sezioni. Inoltre, deve anche essere tollerante nei confronti della natura non monotona dei dati di decadimento.<br> | + | L'integrale di Schroeder non è applicabile all'elaborazione effettuata nel dominio della frequenza. Le porzioni STFT catturano i decadimenti del riverbero e il rumore e i tempi di riverbero possono essere stimati adattando una funzione esponenziale del decadimento più il rumore, alla serie di dati formata dai valori delle porzioni in ogni intervallo di tempo. Il processo di adattamento deve tenere conto dell'effetto della finestra di sinistra sulla serie di dati, dove la sua larghezza è maggiore dell'intervallo delle sezioni. Inoltre, deve anche essere tollerante nei confronti della natura non monotona dei dati di decadimento.<br><br> |
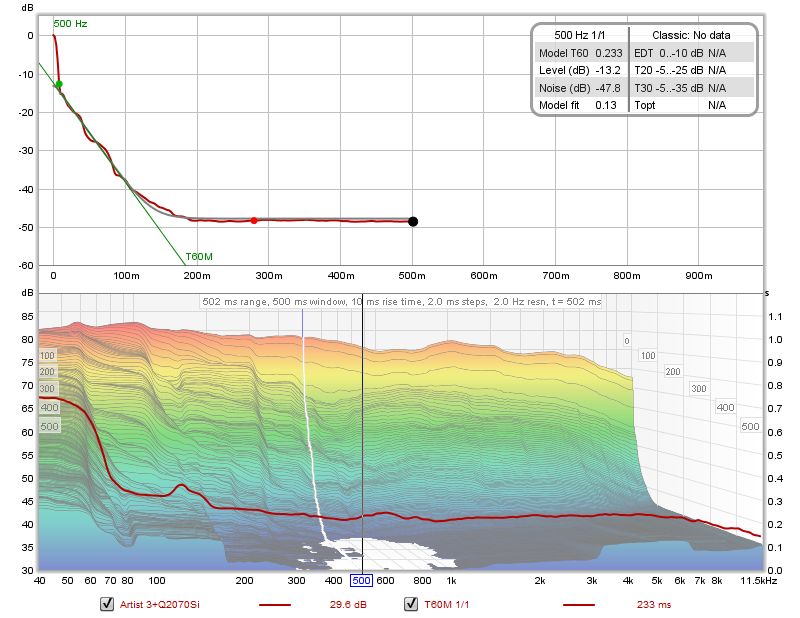
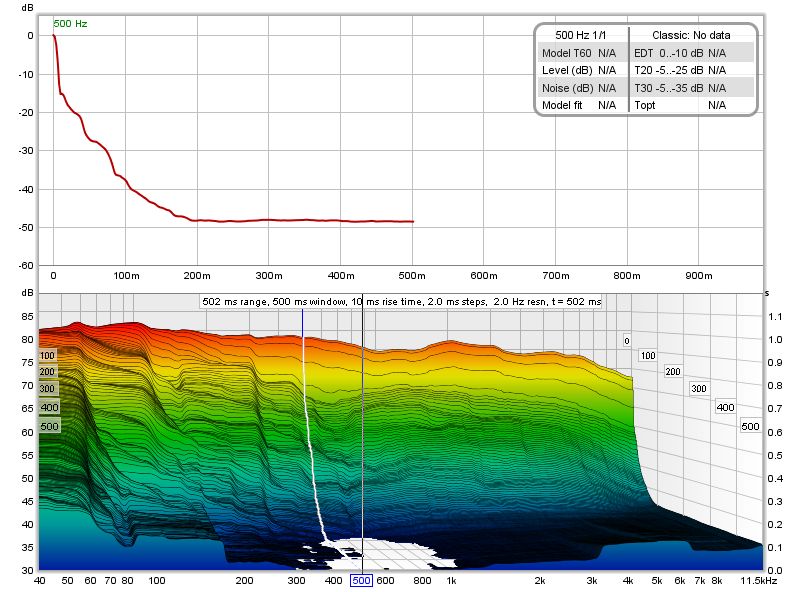
Ecco un esempio di un grafico del decadimento dell'RT60, dopo aver generato i dati STFT (premendo il pulsante '''Generate''' nell'angolo in basso a sinistra nella parte inferiore del grafico), ma prima di calcolare il modello RT60. Il pannello superiore mostra la curva di decadimento riferita alla posizione del cursore nel grafico inferiore. | Ecco un esempio di un grafico del decadimento dell'RT60, dopo aver generato i dati STFT (premendo il pulsante '''Generate''' nell'angolo in basso a sinistra nella parte inferiore del grafico), ma prima di calcolare il modello RT60. Il pannello superiore mostra la curva di decadimento riferita alla posizione del cursore nel grafico inferiore. | ||
Versione delle 18:14, 15 ott 2023
Indice
Grafico del decadimento dell'RT60
Stima dell'RT60 nel dominio della frequenza
- Confronto di selettività
- Confronto di precisione
- Implementazione
Stima classica dell'RT60
Un approccio nel dominio della frequenza alla stima dell'RT60
L'integrale di Schroeder non è applicabile all'elaborazione effettuata nel dominio della frequenza. Le porzioni STFT catturano i decadimenti del riverbero e il rumore e i tempi di riverbero possono essere stimati adattando una funzione esponenziale del decadimento più il rumore, alla serie di dati formata dai valori delle porzioni in ogni intervallo di tempo. Il processo di adattamento deve tenere conto dell'effetto della finestra di sinistra sulla serie di dati, dove la sua larghezza è maggiore dell'intervallo delle sezioni. Inoltre, deve anche essere tollerante nei confronti della natura non monotona dei dati di decadimento.
Ecco un esempio di un grafico del decadimento dell'RT60, dopo aver generato i dati STFT (premendo il pulsante Generate nell'angolo in basso a sinistra nella parte inferiore del grafico), ma prima di calcolare il modello RT60. Il pannello superiore mostra la curva di decadimento riferita alla posizione del cursore nel grafico inferiore.