Grafico del decadimento dell'RT60: differenze tra le versioni
Da REW Wiki.
(→Stima dell'RT60 nel dominio della frequenza) |
|||
| Riga 23: | Riga 23: | ||
:*Implementazione | :*Implementazione | ||
| + | |||
<span style="color:#4076c0;">'''''Stima classica dell'RT60'''''</span> | <span style="color:#4076c0;">'''''Stima classica dell'RT60'''''</span> | ||
Versione delle 17:56, 15 ott 2023
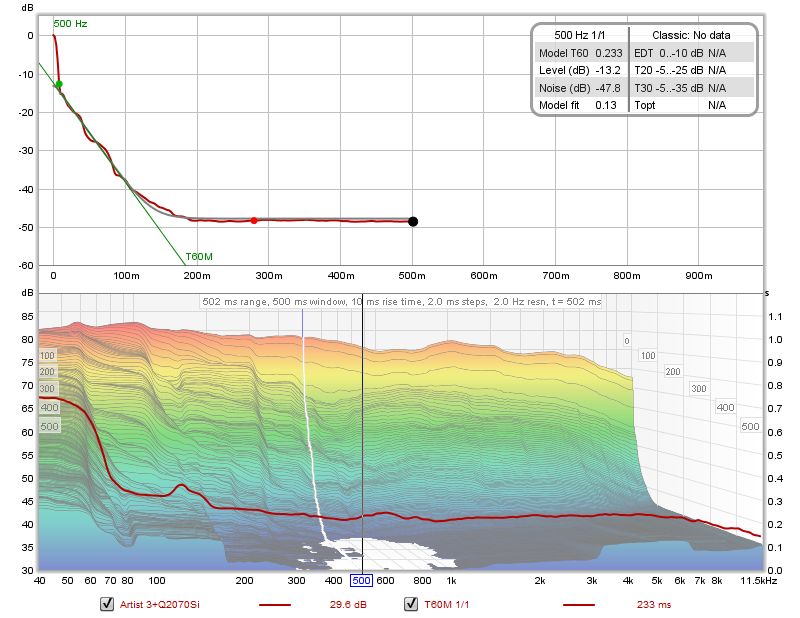
Grafico del decadimento dell'RT60
Il grafico di REW, relativo al decadimento dell'RT60, fornisce un modo per esaminare il comportamento del tempo di riverbero a risoluzioni di frequenza molto più elevate e con frazioni di ottava molto più strette di quanto sia normalmente possibile, anche a basse frequenze, grazie ad un approccio nel dominio della frequenza.
Stima dell'RT60 nel dominio della frequenza
Il grafico di REW, relativo al decadimento dell'RT60, adotta per la stima di quest'ultimo, un approccio nel dominio della frequenza piuttosto che il più consueto approccio nel dominio del tempo.
- Un approccio nel dominio della frequenza alla stima dell'RT60
- Confronto di selettività
- Confronto di precisione
- Implementazione
Stima classica dell'RT60
I tempi di riverbero vengono solitamente determinati mediante l'elaborazione nel dominio del tempo. I vari valori di RT60 vengono stimati calcolando la pendenza dell'integrale di Schroeder, che è un grafico dell'energia (valori al quadrato) della risposta all'impulso integrata all'indietro (sommata partendo dalla fine e muovendosi all'indietro). Le diverse misure RT60 (ad esempio T20, T30, Topt di REW) vengono quindi derivate calcolando la linea di adattamento migliore all'integrale di Schroeder su diversi intervalli. Ci sono alcune limitazioni a questo approccio. Il rumore di fondo della misurazione influenza la forma dell'integrale di Schroeder, facendolo curvare. Vengono applicate varie misure per ridurre tale effetto stimando il livello del rumore di fondo e alterando il punto in cui inizia l'integrazione e i valori iniziali che utilizza. Inoltre, i filtri delle bande d'ottava presentano ritardi di gruppo, che possono influenzare i tempi di riverbero calcolati, soprattutto alle basse frequenze. I filtri solitamente hanno anche una scarsa discriminazione di frequenza, poiché il loro ordine è generalmente basso (tipicamente il 6° ordine) per evitare di esacerbare il problema del ritardo di gruppo. Di conseguenza, forti risonanze hanno un effetto di mascheramento sulle regioni vicine della risposta.