Segnali e misure: differenze tra le versioni
(→Finestratura della Risposta all’Impulso) |
|||
| Riga 5: | Riga 5: | ||
<div align="justify">Per dare un senso a tutte le misure che con REW si possono eseguire, è importante capirne il loro significato. Questo argomento fornisce una panoramica delle nozioni di base dei segnali e delle misure e spiega come sono generati i vari grafici all’interno di REW e come questi sono messi in relazione a quanto è stato misurato.</div> | <div align="justify">Per dare un senso a tutte le misure che con REW si possono eseguire, è importante capirne il loro significato. Questo argomento fornisce una panoramica delle nozioni di base dei segnali e delle misure e spiega come sono generati i vari grafici all’interno di REW e come questi sono messi in relazione a quanto è stato misurato.</div> | ||
| + | ---- | ||
| Riga 13: | Riga 14: | ||
<div align="justify">La '''risoluzione''' delle misure della scheda audio, è tipicamente pari a 16 bit o 24 bit. La risoluzione a 16 bit, è la stessa utilizzata nei CD ed è supportata da REW. Avere 16 bit di risoluzione, significa che l'intervallo dei valori di una misura, è compreso tra -32768 e +32767 (numeri che possono essere rappresentati con 15 cifre binarie, più la 16^ cifra per memorizzare il segno del numero). Anziché utilizzare direttamente i numeri della misura, è conveniente fare riferimento ad essi in termini di quanto si avvicinano al numero più grande riferito al '''Fondo Scala''' (Full Scale) abbreviato come '''FS'''. I valori FS sono -32768 e +32767. Il più piccolo valore di misura diverso da zero, è 1, che, come percentuale del fondo scala, equivale a 100 x (1/32768) o, approssimativamente lo 0.003% FS. Tutto ciò che è più piccolo di questo valore, è visto dalla scheda audio come zero. Il valore di fondo scala, corrisponderà ad una certa tensione agli ingressi della scheda audio, che normalmente si aggira intorno a 1 Volt. Le schede audio che hanno una risoluzione maggiore (24 bit), generalmente accettano la stessa tensione massima (circa 1 Volt), ma possono usare una gamma maggiore di valori per misurare la tensione di ingresso. Per una scheda audio a 24-bit, il numero di valori riferito al FS, varia da -8388608 a +8388607. Questo, rappresenta ancora solo 1 Volt (tipicamente), e non è cambiato ma, data la risoluzione maggiore, il più piccolo valore che può essere rilevato, è pari a 100 x (1/8388608) percentuale del FS, cioè 0.000012% FS. Quindi, la maggior risoluzione offre benefici nella misura di segnali molto piccoli. Il valore di fondo scala è spesso trattato come corrispondente al valore uno e tutto ciò che si trova sotto tale valore rispetto al fondo scala, è considerato come la corrispondente proporzione di uno. Così mezzo fondo scala sarà 0.5 e così via.</div> | <div align="justify">La '''risoluzione''' delle misure della scheda audio, è tipicamente pari a 16 bit o 24 bit. La risoluzione a 16 bit, è la stessa utilizzata nei CD ed è supportata da REW. Avere 16 bit di risoluzione, significa che l'intervallo dei valori di una misura, è compreso tra -32768 e +32767 (numeri che possono essere rappresentati con 15 cifre binarie, più la 16^ cifra per memorizzare il segno del numero). Anziché utilizzare direttamente i numeri della misura, è conveniente fare riferimento ad essi in termini di quanto si avvicinano al numero più grande riferito al '''Fondo Scala''' (Full Scale) abbreviato come '''FS'''. I valori FS sono -32768 e +32767. Il più piccolo valore di misura diverso da zero, è 1, che, come percentuale del fondo scala, equivale a 100 x (1/32768) o, approssimativamente lo 0.003% FS. Tutto ciò che è più piccolo di questo valore, è visto dalla scheda audio come zero. Il valore di fondo scala, corrisponderà ad una certa tensione agli ingressi della scheda audio, che normalmente si aggira intorno a 1 Volt. Le schede audio che hanno una risoluzione maggiore (24 bit), generalmente accettano la stessa tensione massima (circa 1 Volt), ma possono usare una gamma maggiore di valori per misurare la tensione di ingresso. Per una scheda audio a 24-bit, il numero di valori riferito al FS, varia da -8388608 a +8388607. Questo, rappresenta ancora solo 1 Volt (tipicamente), e non è cambiato ma, data la risoluzione maggiore, il più piccolo valore che può essere rilevato, è pari a 100 x (1/8388608) percentuale del FS, cioè 0.000012% FS. Quindi, la maggior risoluzione offre benefici nella misura di segnali molto piccoli. Il valore di fondo scala è spesso trattato come corrispondente al valore uno e tutto ciò che si trova sotto tale valore rispetto al fondo scala, è considerato come la corrispondente proporzione di uno. Così mezzo fondo scala sarà 0.5 e così via.</div> | ||
| + | ---- | ||
| Riga 18: | Riga 20: | ||
Se il segnale è maggiore del valore di fondo scala, la scheda audio non sarà in grado di trattarlo. Il valore della misura non potrà essere in ogni caso maggiore del valore FS, qualsiasi cosa succeda all’ingresso. Quando il segnale è andato al di là dell'intervallo che l’ingresso è in grado di misurare, si dice che è stato '''clippato''' (tagliato). Il clipping è visualizzato sui segnali di ingresso, come una parte piatta della risposta. Se avviene all’ingresso della scheda audio, sarà a +100% FS o a -100% FS e REW vi avviserà, ma talvolta, il clipping avviene prima che il segnale raggiunga la scheda audio (per esempio, nel preamplificatore microfonico, se è stato impostato un guadagno troppo elevato). In questo caso, i valori di misura, non arriveranno mai al valore FS della scheda audio, ma il segnale sarà comunque clippato. Il clipping deve essere evitato durante la misura, perchè il segnale catturato, non rappresenta più ciò che realmente sta accadendo all’ingresso e che corrompe la misura. | Se il segnale è maggiore del valore di fondo scala, la scheda audio non sarà in grado di trattarlo. Il valore della misura non potrà essere in ogni caso maggiore del valore FS, qualsiasi cosa succeda all’ingresso. Quando il segnale è andato al di là dell'intervallo che l’ingresso è in grado di misurare, si dice che è stato '''clippato''' (tagliato). Il clipping è visualizzato sui segnali di ingresso, come una parte piatta della risposta. Se avviene all’ingresso della scheda audio, sarà a +100% FS o a -100% FS e REW vi avviserà, ma talvolta, il clipping avviene prima che il segnale raggiunga la scheda audio (per esempio, nel preamplificatore microfonico, se è stato impostato un guadagno troppo elevato). In questo caso, i valori di misura, non arriveranno mai al valore FS della scheda audio, ma il segnale sarà comunque clippato. Il clipping deve essere evitato durante la misura, perchè il segnale catturato, non rappresenta più ciò che realmente sta accadendo all’ingresso e che corrompe la misura. | ||
| + | ---- | ||
| Riga 31: | Riga 34: | ||
<div align="justify">Quando, per calcolare lo spettro, facciamo uso della FFT, essa usa un pacchetto di frequenze che, uniformemente distanziate, partono dalla DC (frequenza zero) fino alla metà della frequenza di campionamento (il massimo che può essere correttamente rappresentato). La spaziatura, dipende dalla lunghezza del segnale che intendiamo analizzare con la FFT. I calcoli della FFT, sono molto più efficienti, quando le lunghezze dei segnali sono potenze di 2, come 16k (16,384), 32k (32768) o 64k (65536). Per calcolare la FFT a 64k da un segnale che è campionato a 48kHz, abbiamo bisogno di 65536/48000 secondi di segnale, cioè 1.365s. Le frequenze, saranno distanziate di 24000/65536 = 0.366Hz. Se la FFT è stata generata da campioni a 16k, le frequenze saranno distanziate di 1.465Hz. Minore è il numero di campioni utilizzati per generare la FFT, maggiore sarà la distanza tra le frequenze e minore sarà la risoluzione in frequenza. Per un'alta risoluzione in frequenza, dobbiamo analizzare lunghi periodi dei segnali.</div> | <div align="justify">Quando, per calcolare lo spettro, facciamo uso della FFT, essa usa un pacchetto di frequenze che, uniformemente distanziate, partono dalla DC (frequenza zero) fino alla metà della frequenza di campionamento (il massimo che può essere correttamente rappresentato). La spaziatura, dipende dalla lunghezza del segnale che intendiamo analizzare con la FFT. I calcoli della FFT, sono molto più efficienti, quando le lunghezze dei segnali sono potenze di 2, come 16k (16,384), 32k (32768) o 64k (65536). Per calcolare la FFT a 64k da un segnale che è campionato a 48kHz, abbiamo bisogno di 65536/48000 secondi di segnale, cioè 1.365s. Le frequenze, saranno distanziate di 24000/65536 = 0.366Hz. Se la FFT è stata generata da campioni a 16k, le frequenze saranno distanziate di 1.465Hz. Minore è il numero di campioni utilizzati per generare la FFT, maggiore sarà la distanza tra le frequenze e minore sarà la risoluzione in frequenza. Per un'alta risoluzione in frequenza, dobbiamo analizzare lunghi periodi dei segnali.</div> | ||
| + | ---- | ||
| Riga 39: | Riga 43: | ||
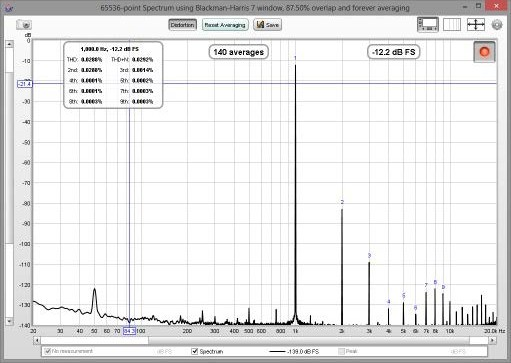
[[File:spettro.png | center]] | [[File:spettro.png | center]] | ||
| + | ---- | ||
| Riga 49: | Riga 54: | ||
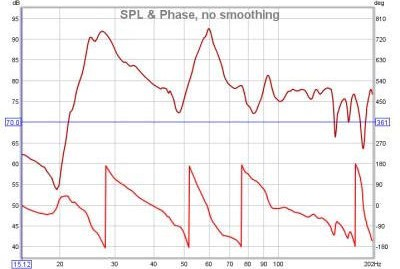
[[File:spl_e_fase.png | center]] | [[File:spl_e_fase.png | center]] | ||
| + | ---- | ||
| Riga 64: | Riga 70: | ||
output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3] | output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3] | ||
E così via per ogni successivo campione che appare. Il prodotto ottenuto dalla moltiplicazione dei campioni del segnale d’ingresso , con i campioni della IR, è chiamato '''convoluzione'''. Tipicamente, per la misurazione di una parte di un apparato, la risposta all’impulso è abbastanza di breve durata, molto meno di un secondo, mentre assume valori di un secondo o due, per la misura di una stanza domestica di medie dimensioni. Così eventualmente l’uscita ad ogni periodo di tempo, è data dalla lunghezza della IR, moltiplicata per la stessa lunghezza del segnale di ingresso, sommata a tutti i singoli prodotti fino ad ottenere l’uscita per quel periodo di tempo.</div> | E così via per ogni successivo campione che appare. Il prodotto ottenuto dalla moltiplicazione dei campioni del segnale d’ingresso , con i campioni della IR, è chiamato '''convoluzione'''. Tipicamente, per la misurazione di una parte di un apparato, la risposta all’impulso è abbastanza di breve durata, molto meno di un secondo, mentre assume valori di un secondo o due, per la misura di una stanza domestica di medie dimensioni. Così eventualmente l’uscita ad ogni periodo di tempo, è data dalla lunghezza della IR, moltiplicata per la stessa lunghezza del segnale di ingresso, sommata a tutti i singoli prodotti fino ad ottenere l’uscita per quel periodo di tempo.</div> | ||
| + | ---- | ||
| Riga 81: | Riga 88: | ||
e così via. L’uscita sarebbe costituita a turno, da ciascun campione della IR. Un segnale di ingresso composto da un singolo campione a fondo scala, seguito da zeri, è chiamato '''impulso'''. Quando il sistema veicola alla sua uscita un simile segnale di ingresso, ciò viene definito ''risposta all’impulso''.</div> | e così via. L’uscita sarebbe costituita a turno, da ciascun campione della IR. Un segnale di ingresso composto da un singolo campione a fondo scala, seguito da zeri, è chiamato '''impulso'''. Quando il sistema veicola alla sua uscita un simile segnale di ingresso, ciò viene definito ''risposta all’impulso''.</div> | ||
| + | ---- | ||
| Riga 86: | Riga 94: | ||
<div align="justify>Poichè la funzione di trasferimento e la risposta all’impulso sono entrambe descrizioni dello stesso sistema, potremmo ragionevolmente supporre che siano tra loro correlate e lo sono. La funzione di trasferimento è la FFT della risposta all’impulso, e la risposta all’impulso è la FFT inversa della funzione di trasferimento. Entrambe sono visioni dello stesso sistema, una nel dominio della frequenza, e l’altra nel dominio del tempo. La funzione di trasferimento, è semplicemente lo spettro della risposta all’impulso.</div> | <div align="justify>Poichè la funzione di trasferimento e la risposta all’impulso sono entrambe descrizioni dello stesso sistema, potremmo ragionevolmente supporre che siano tra loro correlate e lo sono. La funzione di trasferimento è la FFT della risposta all’impulso, e la risposta all’impulso è la FFT inversa della funzione di trasferimento. Entrambe sono visioni dello stesso sistema, una nel dominio della frequenza, e l’altra nel dominio del tempo. La funzione di trasferimento, è semplicemente lo spettro della risposta all’impulso.</div> | ||
| + | ---- | ||
| Riga 95: | Riga 104: | ||
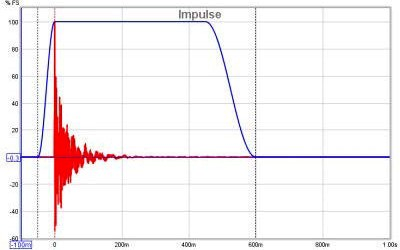
[[File:Impulso.png|center|impulso]]<br>[[File:Impulso_finestrato.png|center|impulso finestrato]] | [[File:Impulso.png|center|impulso]]<br>[[File:Impulso_finestrato.png|center|impulso finestrato]] | ||
| + | ---- | ||
| Riga 102: | Riga 112: | ||
Il viaggio del suono che raggiunge il microfono attraverso un percorso diretto dall’altoparlante, oltre ad essere il più breve, è quello che impiega il minor tempo. L’altoparlante però, irradia il suono anche in altre direzioni che lo fanno rimbalzare sulle varie superfici della stanza. Queste riflessioni, compiendo quindi un tragitto maggiore prima di raggiungere il microfono, impiegano un tempo maggiore prima di arrivare a destinazione. Nel caso di un impulso, questo arriverà prima delle riflessioni, che arriveranno invece ritardate. Questo ritardo, è determinato dal maggior tempo necessario al suono, a compiere un percorso maggiore. Minore è il ritardo, minore è il tempo impiegato dal suono per raggiungere la superficie più vicina (se, per esempio, la superficie più vicina fosse situata a 1 m. di distanza, il suono riflesso raggiungerebbe il microfono circa 3 ms più tardi rispetto al suono diretto proveniente dall’altoparlante).<br> | Il viaggio del suono che raggiunge il microfono attraverso un percorso diretto dall’altoparlante, oltre ad essere il più breve, è quello che impiega il minor tempo. L’altoparlante però, irradia il suono anche in altre direzioni che lo fanno rimbalzare sulle varie superfici della stanza. Queste riflessioni, compiendo quindi un tragitto maggiore prima di raggiungere il microfono, impiegano un tempo maggiore prima di arrivare a destinazione. Nel caso di un impulso, questo arriverà prima delle riflessioni, che arriveranno invece ritardate. Questo ritardo, è determinato dal maggior tempo necessario al suono, a compiere un percorso maggiore. Minore è il ritardo, minore è il tempo impiegato dal suono per raggiungere la superficie più vicina (se, per esempio, la superficie più vicina fosse situata a 1 m. di distanza, il suono riflesso raggiungerebbe il microfono circa 3 ms più tardi rispetto al suono diretto proveniente dall’altoparlante).<br> | ||
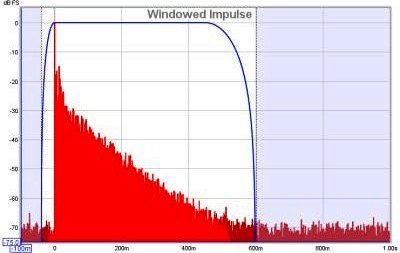
Se dovessimo analizzare solo i primi pochi ms della risposta all’impulso, vedremmo la parte corrispondente all’arrivo iniziale, che proviene direttamente dall’altoparlante, senza il contributo della stanza. Analizzando in questo modo, una piccola porzione della risposta all’impulso, eseguiremmo una '''finestratura''' della risposta (nelle immagini della risposta all’impulso, pochi righe sopra, la traccia blu mostra la finestra). Calcolando una FFT per quella porzione della IR (risposta all’impulso), potremmo vedere la funzione di trasferimento per quell’istante che corrisponderebbe alla funzione di trasferimento del solo altoparlante. Tuttavia, c’è uno svantaggio. Infatti, calcolando una FFT di un segnale breve, potremmo vedere solo la risposta fino a un limite che dipende da quanto lungo era il segnale in esame. Se avessimo un intero secondo di segnale da analizzare, potremmo avere una risposta in frequenza che scende fino a 1Hz mentre, se avessimo un segnale che dura solo 1/10 di secondo, la risposta scenderebbe fino a 10Hz. Generalmente, se la lunghezza del segnale da analizzare, vale T secondi, la frequenza più bassa vale 1/T. Così se la nostra finestra durasse 3ms, la risposta in frequenza scenderebbe solo fino a 1/0.003 = 333Hz. Così, per vedere le risposte a bassa frequenza senza le influenze della stanza, la superficie più vicina deve essere la più lontana possibile.. Per regolare le impostazioni della finestra in REW, cliccare sul pulsante '''IR Windows'''. Per impostazione predefinita, REW usa impostazioni della finestra che includono più di 0.5s della risposta all’impulso, in modo che gli effetti della stanza siano visibili.</div> | Se dovessimo analizzare solo i primi pochi ms della risposta all’impulso, vedremmo la parte corrispondente all’arrivo iniziale, che proviene direttamente dall’altoparlante, senza il contributo della stanza. Analizzando in questo modo, una piccola porzione della risposta all’impulso, eseguiremmo una '''finestratura''' della risposta (nelle immagini della risposta all’impulso, pochi righe sopra, la traccia blu mostra la finestra). Calcolando una FFT per quella porzione della IR (risposta all’impulso), potremmo vedere la funzione di trasferimento per quell’istante che corrisponderebbe alla funzione di trasferimento del solo altoparlante. Tuttavia, c’è uno svantaggio. Infatti, calcolando una FFT di un segnale breve, potremmo vedere solo la risposta fino a un limite che dipende da quanto lungo era il segnale in esame. Se avessimo un intero secondo di segnale da analizzare, potremmo avere una risposta in frequenza che scende fino a 1Hz mentre, se avessimo un segnale che dura solo 1/10 di secondo, la risposta scenderebbe fino a 10Hz. Generalmente, se la lunghezza del segnale da analizzare, vale T secondi, la frequenza più bassa vale 1/T. Così se la nostra finestra durasse 3ms, la risposta in frequenza scenderebbe solo fino a 1/0.003 = 333Hz. Così, per vedere le risposte a bassa frequenza senza le influenze della stanza, la superficie più vicina deve essere la più lontana possibile.. Per regolare le impostazioni della finestra in REW, cliccare sul pulsante '''IR Windows'''. Per impostazione predefinita, REW usa impostazioni della finestra che includono più di 0.5s della risposta all’impulso, in modo che gli effetti della stanza siano visibili.</div> | ||
| + | ---- | ||
| + | |||
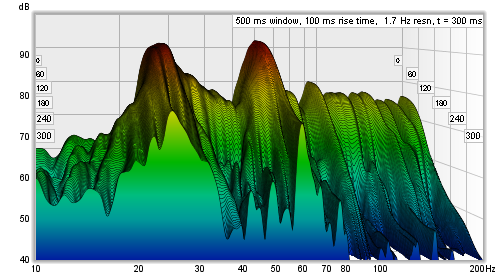
===<span style="color:#00007f; text-decoration: underline;">Waterfall (grafico a cascata)</span>=== | ===<span style="color:#00007f; text-decoration: underline;">Waterfall (grafico a cascata)</span>=== | ||
| Riga 110: | Riga 122: | ||
<div align="justify">Questa è stata una veloce introduzione ai concetti che stanno alla base della teoria dei segnali e delle misure. Se siete riusciti a restare incollati fino alla fine, ben fatto! Ora avete le informazioni necessarie per comprendere meglio come REW [[Iniziare con REW#Come REW esegue le misure|esegue le misure]].</div> | <div align="justify">Questa è stata una veloce introduzione ai concetti che stanno alla base della teoria dei segnali e delle misure. Se siete riusciti a restare incollati fino alla fine, ben fatto! Ora avete le informazioni necessarie per comprendere meglio come REW [[Iniziare con REW#Come REW esegue le misure|esegue le misure]].</div> | ||
| + | ---- | ||
Versione delle 07:55, 6 giu 2016
Indice
[nascondi]- 1 Segnali e Misure
- 1.1 "Cosa significa tutta questa roba?"
- 1.2 Segnali, Frequenza di campionamento e Risoluzione
- 1.3 Clipping
- 1.4 Visualizzare i segnali
- 1.5 RTA (Real Time Analyzer)
- 1.6 Sistemi e Funzioni di Trasferimento
- 1.7 La risposta all’impulso
- 1.8 Perchè è chiamata "risposta all’impulso"?
- 1.9 Relazione tra la Funzione di Trasferimento e la Risposta all’Impulso
- 1.10 Visualizzare la risposta all’impulso
- 1.11 Finestratura della Risposta all’Impulso
- 1.12 Waterfall (grafico a cascata)
Segnali e Misure
"Cosa significa tutta questa roba?"
Segnali, Frequenza di campionamento e Risoluzione
Clipping
Se il segnale è maggiore del valore di fondo scala, la scheda audio non sarà in grado di trattarlo. Il valore della misura non potrà essere in ogni caso maggiore del valore FS, qualsiasi cosa succeda all’ingresso. Quando il segnale è andato al di là dell'intervallo che l’ingresso è in grado di misurare, si dice che è stato clippato (tagliato). Il clipping è visualizzato sui segnali di ingresso, come una parte piatta della risposta. Se avviene all’ingresso della scheda audio, sarà a +100% FS o a -100% FS e REW vi avviserà, ma talvolta, il clipping avviene prima che il segnale raggiunga la scheda audio (per esempio, nel preamplificatore microfonico, se è stato impostato un guadagno troppo elevato). In questo caso, i valori di misura, non arriveranno mai al valore FS della scheda audio, ma il segnale sarà comunque clippato. Il clipping deve essere evitato durante la misura, perchè il segnale catturato, non rappresenta più ciò che realmente sta accadendo all’ingresso e che corrompe la misura.
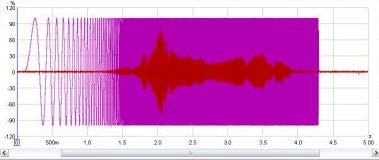
Visualizzare i segnali
RTA (Real Time Analyzer)
Sistemi e Funzioni di Trasferimento
La risposta all’impulso
output[1] = input[1]*IR[1]
Un campione di intervallo più tardi, l’ingresso ha 2 campioni sovrapposti con la IR. L’uscita per questo periodo di tempo è data dal secondo campione di tempo all’ingresso, moltiplicato per il primo campione della IR, più il primo campione di tempo all’ingresso, moltiplicato per il secondo campione della IR:
output[2] = input[2]*IR[1] + input[1]*IR[2]
Un altro campione di intervallo più tardi, l’ingresso ha 3 campioni sovrapposti con la IR. L’uscita sarà: output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3]
E così via per ogni successivo campione che appare. Il prodotto ottenuto dalla moltiplicazione dei campioni del segnale d’ingresso , con i campioni della IR, è chiamato convoluzione. Tipicamente, per la misurazione di una parte di un apparato, la risposta all’impulso è abbastanza di breve durata, molto meno di un secondo, mentre assume valori di un secondo o due, per la misura di una stanza domestica di medie dimensioni. Così eventualmente l’uscita ad ogni periodo di tempo, è data dalla lunghezza della IR, moltiplicata per la stessa lunghezza del segnale di ingresso, sommata a tutti i singoli prodotti fino ad ottenere l’uscita per quel periodo di tempo.
Perchè è chiamata "risposta all’impulso"?
output[1] = input[1]*IR[1] = IR[1]
Il successivo campione sarebbe:
output[2] = input[2]*IR[1] + input[1]*IR[2] = 0*IR[1] + 1*IR[2] = IR[2]
Il terzo campione sarebbe:
output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3] = 0*IR[1] + 0*IR[2] + 1*IR[3] = IR[3]
e così via. L’uscita sarebbe costituita a turno, da ciascun campione della IR. Un segnale di ingresso composto da un singolo campione a fondo scala, seguito da zeri, è chiamato impulso. Quando il sistema veicola alla sua uscita un simile segnale di ingresso, ciò viene definito risposta all’impulso.
Relazione tra la Funzione di Trasferimento e la Risposta all’Impulso
Visualizzare la risposta all’impulso
Finestratura della Risposta all’Impulso
Il viaggio del suono che raggiunge il microfono attraverso un percorso diretto dall’altoparlante, oltre ad essere il più breve, è quello che impiega il minor tempo. L’altoparlante però, irradia il suono anche in altre direzioni che lo fanno rimbalzare sulle varie superfici della stanza. Queste riflessioni, compiendo quindi un tragitto maggiore prima di raggiungere il microfono, impiegano un tempo maggiore prima di arrivare a destinazione. Nel caso di un impulso, questo arriverà prima delle riflessioni, che arriveranno invece ritardate. Questo ritardo, è determinato dal maggior tempo necessario al suono, a compiere un percorso maggiore. Minore è il ritardo, minore è il tempo impiegato dal suono per raggiungere la superficie più vicina (se, per esempio, la superficie più vicina fosse situata a 1 m. di distanza, il suono riflesso raggiungerebbe il microfono circa 3 ms più tardi rispetto al suono diretto proveniente dall’altoparlante).
Waterfall (grafico a cascata)
Indice dei contenuti - Torna su
Copyright © 2010 John Mulcahy All Rights Reserved