Segnali e misure: differenze tra le versioni
(→Waterfall (grafico a cascata)) |
|||
| Riga 2: | Riga 2: | ||
| − | ===<span style="color:#00007f;">"Cosa significa tutta questa roba?"</span>=== | + | ===<span style="color:#00007f; text-decoration: underline;">"Cosa significa tutta questa roba?"</span>=== |
<div align="justify">Per dare un senso a tutte le misure che con REW si possono eseguire, è importante capirne il loro significato. Questo argomento fornisce una panoramica delle nozioni di base dei segnali e delle misure e spiega come sono generati i vari grafici all’interno di REW e come questi sono messi in relazione a quanto è stato misurato.</div> | <div align="justify">Per dare un senso a tutte le misure che con REW si possono eseguire, è importante capirne il loro significato. Questo argomento fornisce una panoramica delle nozioni di base dei segnali e delle misure e spiega come sono generati i vari grafici all’interno di REW e come questi sono messi in relazione a quanto è stato misurato.</div> | ||
| − | ===<span style="color:#00007f;">Segnali, Frequenza di campionamento e Risoluzione</span>=== | + | ===<span style="color:#00007f; text-decoration: underline;">Segnali, Frequenza di campionamento e Risoluzione</span>=== |
<div align="justify">La prima cosa da comprendere è cos'è un segnale, almeno nel contesto di esecuzione di una misura acustica. I segnali a cui noi siamo interessati, sono suoni registrati attraverso un microfono o attraverso un fonometro. La pressione sonora genera nel microfono / fonometro, dei segnali elettrici che vengono catturati dalla nostra scheda audio, che effettua ai suoi ingressi, la misura del livello elettrico. Ogni misura, è indicata come '''campione'''. Quanto spesso i campioni vengono catturati, dipende dalla '''frequenza di campionamento'''. REW supporta frequenze di campionamento di 44.1kHz o 48kHz, che sta ad indicare quante volte la scheda audio cattura il segnale presente ai suoi ingressi: 44.100 o 48.000 volte al secondo. Tre secondi di un segnale campionato a 48kHz, significano una sequenza di 3 x 48.000 = 144.000 valori. La più alta frequenza che può essere catturata ad una data frequenza di campionamento, è pari alla metà di quest’ultima. Abbiamo quindi bisogno almeno di due campioni per ogni ciclo di frequenza per poterla riprodurre. A 48kHz di campionamento, la massima frequenza che possiamo catturare è pari a 24kHz. Le frequenze che superano la metà della frequenza di campionamento, causerebbero aliasing, e apparirebbero più basse di quanto in realtà sono. Per esempio, un segnale a 25KHz, campionato a 48KHz, apparirebbe come un segnale a 23KHz. Per prevenire questo fenomeno, gli ingressi delle schede audio posseggono dei filtri anti-aliasing, che tentano di bloccare i segnali con una frequenza più alta di quella massima catturabile, ma, non essendo pienamente efficaci, dobbiamo sempre considerare il contenuto in frequenza del segnale che stiamo cercando di catturare.</div> | <div align="justify">La prima cosa da comprendere è cos'è un segnale, almeno nel contesto di esecuzione di una misura acustica. I segnali a cui noi siamo interessati, sono suoni registrati attraverso un microfono o attraverso un fonometro. La pressione sonora genera nel microfono / fonometro, dei segnali elettrici che vengono catturati dalla nostra scheda audio, che effettua ai suoi ingressi, la misura del livello elettrico. Ogni misura, è indicata come '''campione'''. Quanto spesso i campioni vengono catturati, dipende dalla '''frequenza di campionamento'''. REW supporta frequenze di campionamento di 44.1kHz o 48kHz, che sta ad indicare quante volte la scheda audio cattura il segnale presente ai suoi ingressi: 44.100 o 48.000 volte al secondo. Tre secondi di un segnale campionato a 48kHz, significano una sequenza di 3 x 48.000 = 144.000 valori. La più alta frequenza che può essere catturata ad una data frequenza di campionamento, è pari alla metà di quest’ultima. Abbiamo quindi bisogno almeno di due campioni per ogni ciclo di frequenza per poterla riprodurre. A 48kHz di campionamento, la massima frequenza che possiamo catturare è pari a 24kHz. Le frequenze che superano la metà della frequenza di campionamento, causerebbero aliasing, e apparirebbero più basse di quanto in realtà sono. Per esempio, un segnale a 25KHz, campionato a 48KHz, apparirebbe come un segnale a 23KHz. Per prevenire questo fenomeno, gli ingressi delle schede audio posseggono dei filtri anti-aliasing, che tentano di bloccare i segnali con una frequenza più alta di quella massima catturabile, ma, non essendo pienamente efficaci, dobbiamo sempre considerare il contenuto in frequenza del segnale che stiamo cercando di catturare.</div> | ||
| Riga 15: | Riga 15: | ||
| − | ===<span style="color:#00007f;">Clipping</span>=== | + | ===<span style="color:#00007f; text-decoration: underline;">Clipping</span>=== |
Se il segnale è maggiore del valore di fondo scala, la scheda audio non sarà in grado di trattarlo. Il valore della misura non potrà essere in ogni caso maggiore del valore FS, qualsiasi cosa succeda all’ingresso. Quando il segnale è andato al di là dell'intervallo che l’ingresso è in grado di misurare, si dice che è stato '''clippato''' (tagliato). Il clipping è visualizzato sui segnali di ingresso, come una parte piatta della risposta. Se avviene all’ingresso della scheda audio, sarà a +100% FS o a -100% FS e REW vi avviserà, ma talvolta, il clipping avviene prima che il segnale raggiunga la scheda audio (per esempio, nel preamplificatore microfonico, se è stato impostato un guadagno troppo elevato). In questo caso, i valori di misura, non arriveranno mai al valore FS della scheda audio, ma il segnale sarà comunque clippato. Il clipping deve essere evitato durante la misura, perchè il segnale catturato, non rappresenta più ciò che realmente sta accadendo all’ingresso e che corrompe la misura. | Se il segnale è maggiore del valore di fondo scala, la scheda audio non sarà in grado di trattarlo. Il valore della misura non potrà essere in ogni caso maggiore del valore FS, qualsiasi cosa succeda all’ingresso. Quando il segnale è andato al di là dell'intervallo che l’ingresso è in grado di misurare, si dice che è stato '''clippato''' (tagliato). Il clipping è visualizzato sui segnali di ingresso, come una parte piatta della risposta. Se avviene all’ingresso della scheda audio, sarà a +100% FS o a -100% FS e REW vi avviserà, ma talvolta, il clipping avviene prima che il segnale raggiunga la scheda audio (per esempio, nel preamplificatore microfonico, se è stato impostato un guadagno troppo elevato). In questo caso, i valori di misura, non arriveranno mai al valore FS della scheda audio, ma il segnale sarà comunque clippato. Il clipping deve essere evitato durante la misura, perchè il segnale catturato, non rappresenta più ciò che realmente sta accadendo all’ingresso e che corrompe la misura. | ||
| − | ===<span style="color:#00007f;">Visualizzare i segnali</span>=== | + | |
| + | ===<span style="color:#00007f; text-decoration: underline;">Visualizzare i segnali</span>=== | ||
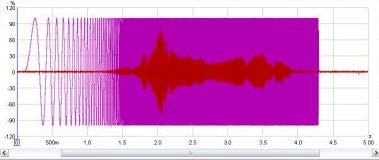
<div align="justify">Un metodo per visualizzare i segnali, è quello di tracciarne i valori rispetto al tempo. Quando i segnali catturati vengono tracciati nel grafico dell’'''oscilloscopio''' di REW, essi vengono mostrati come % '''FS'''. Un segnale che raggiunge il 100% FS, è il più grande segnale che la scheda audio è in grado di catturare. Un esempio dell'oscilloscopio è mostrato qui sotto e visualizza un segnale di sweep generato da REW e (in rosso), la risultante catturata dal microfono.</div> | <div align="justify">Un metodo per visualizzare i segnali, è quello di tracciarne i valori rispetto al tempo. Quando i segnali catturati vengono tracciati nel grafico dell’'''oscilloscopio''' di REW, essi vengono mostrati come % '''FS'''. Un segnale che raggiunge il 100% FS, è il più grande segnale che la scheda audio è in grado di catturare. Un esempio dell'oscilloscopio è mostrato qui sotto e visualizza un segnale di sweep generato da REW e (in rosso), la risultante catturata dal microfono.</div> | ||
| Riga 32: | Riga 33: | ||
| − | ===<span style="color:#00007f;">RTA (Real Time Analyzer)</span>=== | + | ===<span style="color:#00007f; text-decoration: underline;">RTA (Real Time Analyzer)</span>=== |
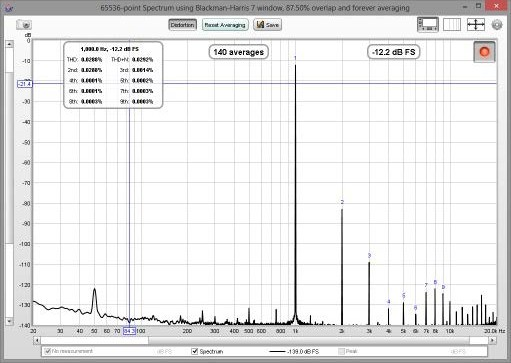
<div align="justify">Un modo comune per visualizzare lo spettro di un segnale di tempo, è l'utilizzo di un Real Time Analyser o RTA. L'RTA mostra un grafico delle ampiezze delle frequenze che costituiscono i segnali che si stanno analizzando. Tuttavia, mentre la FFT produce segnali che sono a frequenze uniformemente distanziate, un RTA le raggruppa insieme in frazioni di ottava. Un'ottava, equivale ad un raddoppio della frequenza, così, l'intervallo tra 100Hz e 200Hz equivale ad un'ottava, così come l'intervallo tra 1kHz e 2kHz. L'intervallo di frequenza di una frazione di ottava, è maggiore della frequenza che si ottiene. Per una RTA a 1/3 di ottava, l'intervallo è di 4.6Hz a 20Hz, ma è di 4.6kHz a 20kHz. Per una RTA a 1/24 di ottava, gli intervalli sono maggiori di 1/8. All'interno dell'intervallo di una frazione di ottava, molti singoli valori FFT possono essere usati per produrre il singolo valore che l'RTA assegna a quella banda di frequenze. In basso, è visualizzata un'immagine dell'RTA di REW che mostra lo spettro di un tono a 1KHz e la sua distorsione armonica.</div> | <div align="justify">Un modo comune per visualizzare lo spettro di un segnale di tempo, è l'utilizzo di un Real Time Analyser o RTA. L'RTA mostra un grafico delle ampiezze delle frequenze che costituiscono i segnali che si stanno analizzando. Tuttavia, mentre la FFT produce segnali che sono a frequenze uniformemente distanziate, un RTA le raggruppa insieme in frazioni di ottava. Un'ottava, equivale ad un raddoppio della frequenza, così, l'intervallo tra 100Hz e 200Hz equivale ad un'ottava, così come l'intervallo tra 1kHz e 2kHz. L'intervallo di frequenza di una frazione di ottava, è maggiore della frequenza che si ottiene. Per una RTA a 1/3 di ottava, l'intervallo è di 4.6Hz a 20Hz, ma è di 4.6kHz a 20kHz. Per una RTA a 1/24 di ottava, gli intervalli sono maggiori di 1/8. All'interno dell'intervallo di una frazione di ottava, molti singoli valori FFT possono essere usati per produrre il singolo valore che l'RTA assegna a quella banda di frequenze. In basso, è visualizzata un'immagine dell'RTA di REW che mostra lo spettro di un tono a 1KHz e la sua distorsione armonica.</div> | ||
| Riga 40: | Riga 41: | ||
| − | ===<span style="color:#00007f;">Sistemi e Funzioni di Trasferimento</span>=== | + | ===<span style="color:#00007f; text-decoration: underline;">Sistemi e Funzioni di Trasferimento</span>=== |
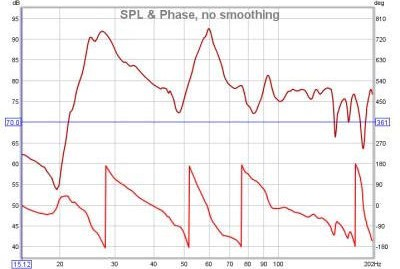
<div align="justify">La visualizzazione di un segnale, ha la sua utilità, ma noi siamo interessati anche a quanto un apparato ''altera'' lo spettro dei segnali. Il modo in cui un sistema modifica lo spettro dei segnali che lo attraversano, è chiamato '''Funzione di Trasferimento'''. La funzione di trasferimento, ha due componenti: la '''Risposta in Frequenza''' e la '''Risposta di Fase'''. La risposta in frequenza, mostra la variazione delle ampiezze delle frequenze introdotte dal sistema, mentre la risposta di fase mostra parimenti la variazione della fase delle frequenze. Una descrizione completa del sistema, richiede entrambe le risposte. Sistemi molto differenti, possono avere la stessa risposta in frequenza, ma la caratteristica che li distingue, è la loro differente risposta di fase.</div><br> | <div align="justify">La visualizzazione di un segnale, ha la sua utilità, ma noi siamo interessati anche a quanto un apparato ''altera'' lo spettro dei segnali. Il modo in cui un sistema modifica lo spettro dei segnali che lo attraversano, è chiamato '''Funzione di Trasferimento'''. La funzione di trasferimento, ha due componenti: la '''Risposta in Frequenza''' e la '''Risposta di Fase'''. La risposta in frequenza, mostra la variazione delle ampiezze delle frequenze introdotte dal sistema, mentre la risposta di fase mostra parimenti la variazione della fase delle frequenze. Una descrizione completa del sistema, richiede entrambe le risposte. Sistemi molto differenti, possono avere la stessa risposta in frequenza, ma la caratteristica che li distingue, è la loro differente risposta di fase.</div><br> | ||
| Riga 50: | Riga 51: | ||
| − | ===<span style="color:#00007f;">La risposta all’impulso</span>=== | + | ===<span style="color:#00007f; text-decoration: underline;">La risposta all’impulso</span>=== |
<div align="justify">La funzione di trasferimento, ci mostra attraverso le risposte di fase e di frequenza, come il sistema influisce sullo spettro del segnale che lo attraversa. Essa caratterizza il sistema in quello che è chiamato '''dominio della frequenza'''. Ma per quanto riguarda il segnale? Come possiamo descrivere come i singoli campioni del segnale vengono modificati dal sistema e il loro comportamento nel '''dominio del tempo'''? Il modo in cui il sistema modifica i campioni di un segnale, è detto '''risposta all’impulso'''. La ragione del nome sarà presto chiara. La risposta all’impulso (IR) è essa stessa un segnale composto da una serie di campioni. I segnali che vengono immessi nel sistema, si sovrappongono alla IR mentre lo attraversano, scorrendo campione per campione. Quando il segnale appare, il suo primo campione sarà allineato con il primo campione della risposta all’impulso. L’uscita del sistema per quel primo campione d’ingresso, è il valore del primo campione della IR, moltiplicato per il valore del primo campione del segnale: | <div align="justify">La funzione di trasferimento, ci mostra attraverso le risposte di fase e di frequenza, come il sistema influisce sullo spettro del segnale che lo attraversa. Essa caratterizza il sistema in quello che è chiamato '''dominio della frequenza'''. Ma per quanto riguarda il segnale? Come possiamo descrivere come i singoli campioni del segnale vengono modificati dal sistema e il loro comportamento nel '''dominio del tempo'''? Il modo in cui il sistema modifica i campioni di un segnale, è detto '''risposta all’impulso'''. La ragione del nome sarà presto chiara. La risposta all’impulso (IR) è essa stessa un segnale composto da una serie di campioni. I segnali che vengono immessi nel sistema, si sovrappongono alla IR mentre lo attraversano, scorrendo campione per campione. Quando il segnale appare, il suo primo campione sarà allineato con il primo campione della risposta all’impulso. L’uscita del sistema per quel primo campione d’ingresso, è il valore del primo campione della IR, moltiplicato per il valore del primo campione del segnale: | ||
| Riga 65: | Riga 66: | ||
| − | ===<span style="color:#00007f;">Perchè è chiamata "risposta all’impulso"?</span>=== | + | ===<span style="color:#00007f; text-decoration: underline;">Perchè è chiamata "risposta all’impulso"?</span>=== |
<div align="justify">Che risultato otterremmo, se il segnale d’ingresso consistesse in un singolo campione a fondo scala, al quale abbiamo assegnato il valore uno, seguito da valori pari a zero per tutti gli altri campioni? Il campione iniziale risultante sarebbe: | <div align="justify">Che risultato otterremmo, se il segnale d’ingresso consistesse in un singolo campione a fondo scala, al quale abbiamo assegnato il valore uno, seguito da valori pari a zero per tutti gli altri campioni? Il campione iniziale risultante sarebbe: | ||
| Riga 82: | Riga 83: | ||
| − | ===<span style="color:#00007f;">Relazione tra la Funzione di Trasferimento e la Risposta all’Impulso</span>=== | + | ===<span style="color:#00007f; text-decoration: underline;">Relazione tra la Funzione di Trasferimento e la Risposta all’Impulso</span>=== |
<div align="justify>Poichè la funzione di trasferimento e la risposta all’impulso sono entrambe descrizioni dello stesso sistema, potremmo ragionevolmente supporre che siano tra loro correlate e lo sono. La funzione di trasferimento è la FFT della risposta all’impulso, e la risposta all’impulso è la FFT inversa della funzione di trasferimento. Entrambe sono visioni dello stesso sistema, una nel dominio della frequenza, e l’altra nel dominio del tempo. La funzione di trasferimento, è semplicemente lo spettro della risposta all’impulso.</div> | <div align="justify>Poichè la funzione di trasferimento e la risposta all’impulso sono entrambe descrizioni dello stesso sistema, potremmo ragionevolmente supporre che siano tra loro correlate e lo sono. La funzione di trasferimento è la FFT della risposta all’impulso, e la risposta all’impulso è la FFT inversa della funzione di trasferimento. Entrambe sono visioni dello stesso sistema, una nel dominio della frequenza, e l’altra nel dominio del tempo. La funzione di trasferimento, è semplicemente lo spettro della risposta all’impulso.</div> | ||
| − | ===<span style="color:#00007f;">Visualizzare la risposta all’impulso</span>=== | + | ===<span style="color:#00007f; text-decoration: underline;">Visualizzare la risposta all’impulso</span>=== |
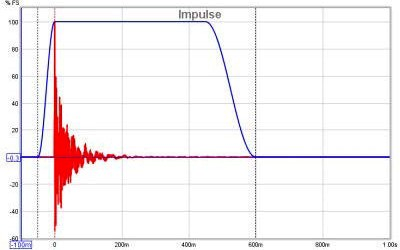
<div align="justify">Il grafico dell'impulso di REW, visualizza la risposta all’impulso. Questo mostra i valori espressi in % FS o in '''dB FS'''. La scala in dB, è utile per visualizzare una dinamica più ampia del segnale e, anzichè tracciare i valori direttamente, traccia il log in base 10 dei valori, moltiplicato per 20. La parte superiore del grafico in dB, equivale a 0dB FS, che corrisponde al 100% FS. Ad un livello del 50% FS, corrisponde 20*log(0.5) = -6dB FS. Il 10% FS equivale a 20*log(0.1) = -20dB FS. La scala in dB FS, è utile per vedere come si comporta l’impulso ai livelli più bassi e dove sparisce sotto il livello di rumore della misura. | <div align="justify">Il grafico dell'impulso di REW, visualizza la risposta all’impulso. Questo mostra i valori espressi in % FS o in '''dB FS'''. La scala in dB, è utile per visualizzare una dinamica più ampia del segnale e, anzichè tracciare i valori direttamente, traccia il log in base 10 dei valori, moltiplicato per 20. La parte superiore del grafico in dB, equivale a 0dB FS, che corrisponde al 100% FS. Ad un livello del 50% FS, corrisponde 20*log(0.5) = -6dB FS. Il 10% FS equivale a 20*log(0.1) = -20dB FS. La scala in dB FS, è utile per vedere come si comporta l’impulso ai livelli più bassi e dove sparisce sotto il livello di rumore della misura. | ||
| Riga 96: | Riga 97: | ||
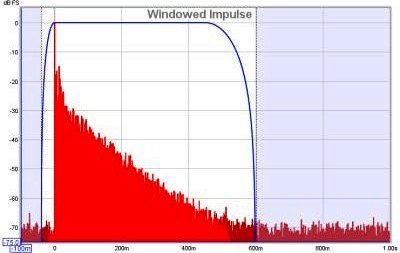
| − | ===<span style="color:#00007f;">Finestratura della Risposta all’Impulso</span>=== | + | ===<span style="color:#00007f; text-decoration: underline;">Finestratura della Risposta all’Impulso</span>=== |
<div align="justify">Supponiamo di voler eseguire una misura su un dispositivo che potrebbe essere un altoparlante, ma in acustica, il sistema che stiamo misurando, comprende altre variabili che intervengono nel percorso tra il segnale generato per la misurazione e il segnale prelevato per l’analisi. Queste variabili, includono gli amplificatori, il microfono, la scheda audio e soprattutto, la stanza stessa. Quindi il sistema nel suo complesso comprende tutti questi elementi e, per poterci concentrare solo su uno di essi, dovremo conoscere un modo per rimuovere l’influenza di tutte quelle parti alle quali non siamo interessati. La risposta della scheda audio, può essere calibrata misurandola separatamente, così come la risposta del microfono, mentre la rimozione degli effetti della stanza è molto più difficoltosa. Potrebbe essere proprio questa che a noi interessa, specialmente se stiamo studiando cosa sentiamo nella nostra posizione di ascolto ma, se cerchiamo di isolare le prestazioni di un altoparlante, il contributo della stanza potrebbe oscurare i dettagli che questo è in grado di riprodurre.<br> | <div align="justify">Supponiamo di voler eseguire una misura su un dispositivo che potrebbe essere un altoparlante, ma in acustica, il sistema che stiamo misurando, comprende altre variabili che intervengono nel percorso tra il segnale generato per la misurazione e il segnale prelevato per l’analisi. Queste variabili, includono gli amplificatori, il microfono, la scheda audio e soprattutto, la stanza stessa. Quindi il sistema nel suo complesso comprende tutti questi elementi e, per poterci concentrare solo su uno di essi, dovremo conoscere un modo per rimuovere l’influenza di tutte quelle parti alle quali non siamo interessati. La risposta della scheda audio, può essere calibrata misurandola separatamente, così come la risposta del microfono, mentre la rimozione degli effetti della stanza è molto più difficoltosa. Potrebbe essere proprio questa che a noi interessa, specialmente se stiamo studiando cosa sentiamo nella nostra posizione di ascolto ma, se cerchiamo di isolare le prestazioni di un altoparlante, il contributo della stanza potrebbe oscurare i dettagli che questo è in grado di riprodurre.<br> | ||
| Riga 103: | Riga 104: | ||
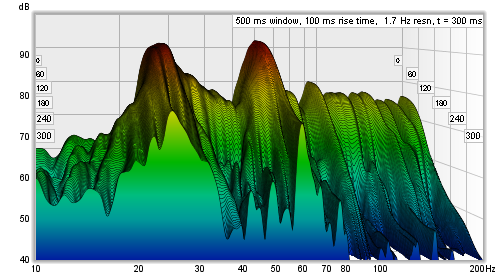
| − | ===<span style="color:#00007f;">Waterfall (grafico a cascata)</span>=== | + | ===<span style="color:#00007f; text-decoration: underline;">Waterfall (grafico a cascata)</span>=== |
<div align="justify">I grafici relativi alla SPL, alla Fase e all’Impulso, sono i più utilizzati per lo studio della funzione di trasferimento che abbiamo catturato, ma esiste un altro grafico che ci fornisce utili informazioni sul comportamento della stanza rispetto al suono in essa riprodotto. Tale grafico è detto '''Waterfall''', e mostra come lo spettro di una sezione della risposta all’impulso cambia, man mano che il tempo progredisce. Esso è ottenuto, finestrando una parte iniziale della risposta, tipicamente pochi centesimi di ms guardando alle risposte della stanza, e la FFT di quella sezione finestrata. La FFT, produce la prima fetta del grafico a cascata. Spostiamo quindi leggermente la finestra lungo la risposta all’impulso, per ottenere la seconda fetta del grafico. Spostiamo ancora leggermente la finestra, per ottenere la terza fetta, poi la quarta e così via. Man mano che ci muoviamo in avanti sul grafico a cascata, iniziamo a perdere il contributo iniziale dato dall’altoparlante e iniziamo a vedere il contributo dato dalla stanza. La risposta di quest’ultima, è più forte a frequenze dove ci sono '''risonanze modali''', che sono frequenze alle quali il suono rimbalza avanti e indietro tra le pareti della stanza, rinforzandosi e producendo uno stabile e lento decadimento. Queste frequenze sono mostrate nel grafico come creste. Più le creste sono alte, peggiori sono le risonanze modali, con lunghi tempi di decadimento.</div> | <div align="justify">I grafici relativi alla SPL, alla Fase e all’Impulso, sono i più utilizzati per lo studio della funzione di trasferimento che abbiamo catturato, ma esiste un altro grafico che ci fornisce utili informazioni sul comportamento della stanza rispetto al suono in essa riprodotto. Tale grafico è detto '''Waterfall''', e mostra come lo spettro di una sezione della risposta all’impulso cambia, man mano che il tempo progredisce. Esso è ottenuto, finestrando una parte iniziale della risposta, tipicamente pochi centesimi di ms guardando alle risposte della stanza, e la FFT di quella sezione finestrata. La FFT, produce la prima fetta del grafico a cascata. Spostiamo quindi leggermente la finestra lungo la risposta all’impulso, per ottenere la seconda fetta del grafico. Spostiamo ancora leggermente la finestra, per ottenere la terza fetta, poi la quarta e così via. Man mano che ci muoviamo in avanti sul grafico a cascata, iniziamo a perdere il contributo iniziale dato dall’altoparlante e iniziamo a vedere il contributo dato dalla stanza. La risposta di quest’ultima, è più forte a frequenze dove ci sono '''risonanze modali''', che sono frequenze alle quali il suono rimbalza avanti e indietro tra le pareti della stanza, rinforzandosi e producendo uno stabile e lento decadimento. Queste frequenze sono mostrate nel grafico come creste. Più le creste sono alte, peggiori sono le risonanze modali, con lunghi tempi di decadimento.</div> | ||
Versione delle 10:22, 3 giu 2016
Indice
[nascondi]- 1 Segnali e Misure
- 1.1 "Cosa significa tutta questa roba?"
- 1.2 Segnali, Frequenza di campionamento e Risoluzione
- 1.3 Clipping
- 1.4 Visualizzare i segnali
- 1.5 RTA (Real Time Analyzer)
- 1.6 Sistemi e Funzioni di Trasferimento
- 1.7 La risposta all’impulso
- 1.8 Perchè è chiamata "risposta all’impulso"?
- 1.9 Relazione tra la Funzione di Trasferimento e la Risposta all’Impulso
- 1.10 Visualizzare la risposta all’impulso
- 1.11 Finestratura della Risposta all’Impulso
- 1.12 Waterfall (grafico a cascata)
Segnali e Misure
"Cosa significa tutta questa roba?"
Segnali, Frequenza di campionamento e Risoluzione
Clipping
Se il segnale è maggiore del valore di fondo scala, la scheda audio non sarà in grado di trattarlo. Il valore della misura non potrà essere in ogni caso maggiore del valore FS, qualsiasi cosa succeda all’ingresso. Quando il segnale è andato al di là dell'intervallo che l’ingresso è in grado di misurare, si dice che è stato clippato (tagliato). Il clipping è visualizzato sui segnali di ingresso, come una parte piatta della risposta. Se avviene all’ingresso della scheda audio, sarà a +100% FS o a -100% FS e REW vi avviserà, ma talvolta, il clipping avviene prima che il segnale raggiunga la scheda audio (per esempio, nel preamplificatore microfonico, se è stato impostato un guadagno troppo elevato). In questo caso, i valori di misura, non arriveranno mai al valore FS della scheda audio, ma il segnale sarà comunque clippato. Il clipping deve essere evitato durante la misura, perchè il segnale catturato, non rappresenta più ciò che realmente sta accadendo all’ingresso e che corrompe la misura.
Visualizzare i segnali
RTA (Real Time Analyzer)
Sistemi e Funzioni di Trasferimento
La risposta all’impulso
output[1] = input[1]*IR[1]
Un campione di intervallo più tardi, l’ingresso ha 2 campioni sovrapposti con la IR. L’uscita per questo periodo di tempo è data dal secondo campione di tempo all’ingresso, moltiplicato per il primo campione della IR, più il primo campione di tempo all’ingresso, moltiplicato per il secondo campione della IR:
output[2] = input[2]*IR[1] + input[1]*IR[2]
Un altro campione di intervallo più tardi, l’ingresso ha 3 campioni sovrapposti con la IR. L’uscita sarà: output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3]
E così via per ogni successivo campione che appare. Il prodotto ottenuto dalla moltiplicazione dei campioni del segnale d’ingresso , con i campioni della IR, è chiamato convoluzione. Tipicamente, per la misurazione di una parte di un apparato, la risposta all’impulso è abbastanza di breve durata, molto meno di un secondo, mentre assume valori di un secondo o due, per la misura di una stanza domestica di medie dimensioni. Così eventualmente l’uscita ad ogni periodo di tempo, è data dalla lunghezza della IR, moltiplicata per la stessa lunghezza del segnale di ingresso, sommata a tutti i singoli prodotti fino ad ottenere l’uscita per quel periodo di tempo.
Perchè è chiamata "risposta all’impulso"?
output[1] = input[1]*IR[1] = IR[1]
Il successivo campione sarebbe:
output[2] = input[2]*IR[1] + input[1]*IR[2] = 0*IR[1] + 1*IR[2] = IR[2]
Il terzo campione sarebbe:
output[3] = input[3]*IR[1] + input[2]*IR[2] + input[1]*IR[3] = 0*IR[1] + 0*IR[2] + 1*IR[3] = IR[3]
e così via. L’uscita sarebbe costituita a turno, da ciascun campione della IR. Un segnale di ingresso composto da un singolo campione a fondo scala, seguito da zeri, è chiamato impulso. Quando il sistema veicola alla sua uscita un simile segnale di ingresso, ciò viene definito risposta all’impulso.
Relazione tra la Funzione di Trasferimento e la Risposta all’Impulso
Visualizzare la risposta all’impulso
Finestratura della Risposta all’Impulso
Il viaggio del suono che raggiunge il microfono attraverso un percorso diretto dall’altoparlante, oltre ad essere il più breve, è quello che impiega il minor tempo. L’altoparlante però, irradia il suono anche in altre direzioni che lo fanno rimbalzare sulle varie superfici della stanza. Queste riflessioni, compiendo quindi un tragitto maggiore prima di raggiungere il microfono, impiegano un tempo maggiore prima di arrivare a destinazione. Nel caso di un impulso, questo arriverà prima delle riflessioni, che arriveranno invece ritardate. Questo ritardo, è determinato dal maggior tempo necessario al suono, a compiere un percorso maggiore. Minore è il ritardo, minore è il tempo impiegato dal suono per raggiungere la superficie più vicina (se, per esempio, la superficie più vicina fosse situata a 1 m. di distanza, il suono riflesso raggiungerebbe il microfono circa 3 ms più tardi rispetto al suono diretto proveniente dall’altoparlante).
Waterfall (grafico a cascata)
Indice dei contenuti - Torna su
Copyright © 2010 John Mulcahy All Rights Reserved